|
1.指出圆的两种定义,各部分名称?等圆、同心圆的
概念?点和圆的位置关系?
2.确定一个圆的基本条件是什么?经过一点可以作几
条直线,几个圆?经过两点可以作几条直线,几个圆?经过两点且使所画的圆的半径等与定长能画几个?
经过三点可以作几条直线,几个圆?
3.展示幻灯片,问:有一个破损的圆形铁轮(课本P62图),现要重新浇铸一个,使它和原来的形状和大小一样,需要先画出铁轮轮廓线的圆,怎样画出这个圆呢?这就是这节课的任务。
[板书]3.1圆(2)-经过三点的圆。
1.在教师指导下,得到以下结论:(为得出定理打好基础)
(])经过一个已知点可以画无数个圆.
(2)经过两个已知点可以画无数个圆,这样的圆的圆心在连结两个已知点所得线段的中垂线上.(板书这一结论)
(3)经过同在一条直线上的三个点不能画圆.
2.定理:不在同一直线上的三个点确定一个圆。
(1)问:经过同一直线上的三个点不能画圆,那么,经过不在同一直线上的三个点能否画圆?能画几个呢?
(2)例 已知不在同一直线上的三个点A、B、C,画⊙O,使它经过点A,B,C.
分析 本题的关键在于找圆心O和确定半径,前面练习中已知,要使⊙O经过点A、B,则点O必须在AB的中垂线上;要使⊙O经过点A、C,则点O又必须在AC的中垂线上.所以,圆心O是线段AB、AC的中垂线的交点.
由于OA=OB=OC,所以半径为OA,OB,OC任取一条.
画法:1.连结AB,AC.
2.画AB、AC的中垂线,相交于O.
3.以O为圆心,OA为半径画⊙O.
∴⊙O就是所求的圆.
(3)教师指出:若连结OB、OC,则因为OB=OC,所以点O又必须在BC的中垂线上.因而,三角形三边的中垂线相交于一点.
因为线段AB、AC的中垂线的交点只有惟一点O,半径0A也是大小确定的.因而,经过不在同一直线上的三个点可以画而且只能画一个圆.
(4)板书定理,并强调定理中的“确定”包含两层含义:即经过不在同一直线上的三个点可以画而且只能画一个圆.(教师简略说明,有四点或四点以上不一定可以画圆)
3.经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.例如:上图中,⊙O是△ABC的外接圆,△ABC是⊙O的内接三角形,点O是△ABC的外心.
注意:外心实际上三角形三边中垂线的交点,它到三角形三个顶点的距离相等。
练习:(比一比,赛一赛)画锐角三角形、钝角三角形、直角三角形的外接圆.
(简要说明直角三角形外心是斜边的中点的推理根据)
6.例 如图所示,已知△ABC内接于⊙O,AB=AC=5,BC=8.求⊙O的半径.
解:连结OA,OB,OC,设OB交BC于D,
∵AB=AC,则点A在BC的中垂线上.
又∵OD=OC,则点O也在BC的中垂线上.
根据两点确定一条直线得,AO垂直平分BC,
∴BD=DC=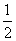 BC=4. BC=4.
由勾股定理得,AD=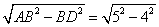 =3,从而,⊙O的半径R= =3,从而,⊙O的半径R=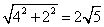 . .
练习:完成P62课内练习和探究活动。
视时间完成P62的作业题
1.定理。
2.从存在性和惟一性两方面理解定理.
1.判断(1)经过三点总可以画一个圆
(2)经过两点的圆的圆心有无数个,但它们都在一条直线上
(3)如果A,B,C三点分别在圆O上,那么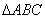 是圆O的外接三角形 是圆O的外接三角形
(4)锐角三角形的外心在三角形内,直角三角形的外心在斜边上,钝角三角形的外心在三角形外
2.填空题(1)确定圆的位置的是 ,确定圆的大小的是
(2)三角形的外心是三角形的 线的交点,它到三角形的 的距离相等
(3)以线段AB为弦能画 圆
(4)在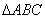 所在平面上,到顶点A,B,C距离都相等的点的个数是 所在平面上,到顶点A,B,C距离都相等的点的个数是
(5)如图,A,B,C,D是 O上的四点,图中 O上的四点,图中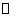 O的内接三角形有 个 O的内接三角形有 个
(6)边长为a的等边三角形的外接圆的半径为
3.A,B,C是三个已知点,根据下列条件说明它们能否确定一个圆。若能确定,求出圆的半径。
(1)AB=3cm,BC=4cm,AC=5cm
(2)AB=2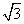 cm,BC=2 cm,BC=2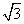 cm,AC=2 cm,AC=2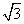 cm cm
(3)AB=2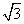 cm,BC=( cm,BC=(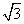 + +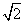 )cm, )cm,
AC=(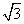 - -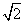 )cm )cm
4.画图(1)已知 ,找出 ,找出 所在圆的圆心O 所在圆的圆心O
(2)已知点A,B及线段r。画半径为r的圆O,使它经过A,B两点。
提高练习
1 如果一个三角形的外心恰好在它的一边的中线上,那么这个三角形一定是( )(A)直角三角形(B)等腰三角形(C)等边三角形(D)性状不能唯一确定
2.已知点A,B在直线l的两侧,那么经过A,B且圆心在l上的圆的个数是( )(A)0(B)1(C)无数个(D)0个,或1个或无数个
3.当锐角三角形ABC的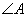 逐渐增大时,它的外心逐渐向 边移动,当 逐渐增大时,它的外心逐渐向 边移动,当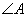 增大到 增大到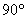 时外心在 处 时外心在 处 |

