|
思考归纳
导入概念 |
如果一个数的平方等于9,这个数是多少?
学生思考并讨论,使学生明白这样的数有两个,它们是3和-3.受前面知识的影响学生可能不易想到-3这个数,这时可提醒学生,这里的这个数可以是负数.注意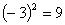 中括号的作用. 中括号的作用.
又如: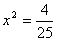 ,则x等于多少呢? ,则x等于多少呢?
使学生完成课本165页的填表练习.
给出平方根的概念:如果一个数的平方等于a,那么这个数就叫做a的平方根.即:如果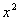 =a,那么x叫做a的平方根. =a,那么x叫做a的平方根.
求一个数的平方根的运算,叫做开平方.
例如: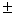 3的平方等于9,9的平方根是 3的平方等于9,9的平方根是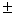 3,所以平方与开平方互为逆运算. 3,所以平方与开平方互为逆运算.
观察:课本中的图13.1-2.
图10.1-2中的两个图描述了平方与开平方互为逆运算的运算过程,揭示了开平方运算的本质.
让学生体验平方和开平方的互逆关系,并根据这个关系说出1,4,9的平方根.
注意:这阶段主要是让学生建立平方根的概念,先不引入平方根的符号,给出的数是完全平方数.
例1:(课本的例4)。求下列各数的平方根。
(1) 100 (2) 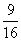 (3) 0.25 (3) 0.25
建议教师要规范书写格式。 |
这个思考题是引入平方根概念的切入点,要让学生有充分的时间进行思考和体验.
在等式中求出x的值,为填表做准备.
通过填表中的x的值,进一步加深时“两个互为相反数的平方等于同一个数”的印象,为平方根的引入做准备.
教学中可以引导学生通过查阅资料等方式,了解平方根产
生发展的过程.(通常称为平方根.在研究有关n次方根的问题
时,为使各次方根的说法协调起见,常采用二次方根的说法.
3表示+3和一3两个数.这种写法学生不太习惯,在以后的教学中宜不断提到。
通过此例使学生明白平方根可以从平方运算中求得,并能规范地表述一个数的平方根.这个例题也为后面探讨平方根的特征做好准备. |

