|
一元二次方程是初中数学的重点内容,学好一元二次方程意义深远。许多同学由于对这一部分内容理解不透,知识掌握不系统,以致学习中形成很大的学习障碍,常出现畏难情绪。根据笔者的教学经验,我们认为学好一元二次方程应注意以下几个方面。
一、理解一个概念
学习一元二次方程,首先要认识一元二次方程,课本中给出的定义是:“在整式方程中,只含有一个未知数,并且未知数的最高次数是2的方程叫做一元二次方程”。其中包含三个方面的意思:一是方程中只含有一个未知数(未知数唯一),二是未知数的最大指数是2,二次项系数不等于0;三是一元二次方程的整式方程(而非分式方程)。此三者缺一不可,其一般形式为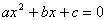 (a≠0)。判断一个方程是否是一元二次方程,要将方程化为一般式。 (a≠0)。判断一个方程是否是一元二次方程,要将方程化为一般式。
例1. 下列方程中,是一元二次方程的是( )
A. 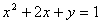
B. 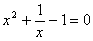
C. 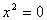
D. 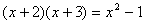
分析:方程(A)含有两个未知数,方程(B)左边是分式,方程(D)整理后是5x+7=0,是一元一次方程。(答案为C)
例2. 关于x的方程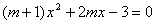 是一元二次方程,则m的取值范围是___________。 是一元二次方程,则m的取值范围是___________。
解:据一元二次方程定义可知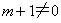
即 。 。
二、掌握四种解法
一元二次方程的解法是这一部分内容的重点。一元二次方程有四种解法:即直接开平方法、配方法、公式法、因式分解法,其基本思想是降次。四种解法又各有特点,只有准确把握,解方程时才会得心应手。
直接开平方法适宜于解形如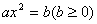 的方程;配方法与公式法是通法,适合任何形式的一元二次方程,其中求根公式的条件是 的方程;配方法与公式法是通法,适合任何形式的一元二次方程,其中求根公式的条件是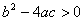 。而因式分解法适合的方程是: 。而因式分解法适合的方程是:
一边为零而另一边易于分解成两个一次因式的积的方程(其依据是若ab=0,则a=0,或b=0)。在遇到不同形式的方程时,要根据方程的特点选择恰当的方法求解。
例3. 方程①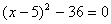 ② ②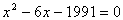 ③ ③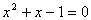 ④ ④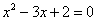 分别适宜于直接开平方法、配方法、公式法、因式分解法。 分别适宜于直接开平方法、配方法、公式法、因式分解法。
|

