一.复习目标:
1.了解映射的概念,理解函数的概念。
2.了解函数的单调性和奇偶性的概念,掌握判断一些简单函数的单调性和奇偶性的方法,并能利用函数的性质简化函数图象的绘制过程。
3.了解反函数的概念及互为反函数的函数图象间的关系,会求一些简单函数的反函数。
4.理解分数指数的概念,掌握有理指数幂的运算性质,掌握指数函数的概念、图象和性质。
5.理解对数的概念,掌握对数的运算性质,掌握对数函数的概念、图象和性质。
6.能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题。
二.考试要求:
1.灵活运用函数概念、性质和不等式等知识以及分类讨论等方法,解函数综合题。
2.应用函数知识及思想方法,解决函数的最值问题、探索性问题与应用性问题,提高分析问题和解决问题的能力。
三.教学过程:
(Ⅰ)2004年高考数学函数综合题选
1.(2004高考广东卷,19)设函数
(1) 证明: 当0< a < b ,且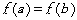 时,ab >1; 时,ab >1; (2) 点P (x0, y0 ) (0< x0 <1 )在曲线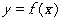 上,求曲线在点P处的切线与x轴 上,求曲线在点P处的切线与x轴 |

