|
高三数学(人教版)第一轮复习单元讲座
第3讲 函数的基本性质
一.课标要求
1.通过已学过的函数特别是二次函数,理解函数的单调性、最大(小)值及其几何意义;
2.结合具体函数,了解奇偶性的含义;
二.命题走向
从近几年来看,函数性质是高考命题的主线索,不论是何种函数,必须与函数性质相关联,因此在复习中,针对不同的函数类别及综合情况,归纳出一定的复习线索。
预测今年高考的出题思路是:通过研究函数的定义域、值域,进而研究函数的单调性、奇偶性以及最值。
预测明年的对本讲的考察是:
(1)考察函数性质的选择题1个或1个填空题,还可能结合导数出研究函数性质的大题;
(2)以中等难度、题型新颖的试题综合考察函数的性质,以组合形式、一题多角度考察函数性质预计成为新的热点。
三.要点精讲
1.奇偶性
(1)定义:如果对于函数f(x)定义域内的任意x都有f(-x)=-f(x),则称f(x)为奇函数;如果对于函数f(x)定义域内的任意x都有f(-x)=f(x),则称f(x)为偶函数。
如果函数f(x)不具有上述性质,则f(x)不具有奇偶性.如果函数同时具有上述两条性质,则f(x)既是奇函数,又是偶函数。
注意:
1 函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
2 由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称)。
(2)利用定义判断函数奇偶性的格式步骤:
1 首先确定函数的定义域,并判断其定义域是否关于原点对称;
2 确定f(-x)与f(x)的关系;
3 作出相应结论:
若f(-x) = f(x) 或 f(-x)-f(x) = 0,则f(x)是偶函数;
若f(-x) =-f(x) 或 f(-x)+f(x) = 0,则f(x)是奇函数。
(3)简单性质:
①图象的对称性质:一个函数是奇函数的充要条件是它的图象关于原点对称;一个函数是偶函数的充要条件是它的图象关于y轴对称;
②设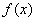 , ,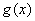 的定义域分别是 的定义域分别是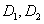 ,那么在它们的公共定义域上: ,那么在它们的公共定义域上:
奇+奇=奇,奇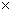 奇=偶,偶+偶=偶,偶 奇=偶,偶+偶=偶,偶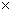 偶=偶,奇 偶=偶,奇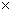 偶=奇 偶=奇 |

