|
空间向量帮你准确定位
立体几何中常出现点的存在性和位置有待于确定的问题.以“是否存在”、“是否有”、“在何位置”等形式的疑问句设问,以示结论有待于确定.传统方法解答此类问题的思路是:首先假设点存在或猜测点的位置,再进行推证,若推出矛盾,即可知该点不存在;若推出合理结论,则可确定该点存在或猜测结果成立.假设和猜测本身难度不大,但严密的逻辑思维和合理的推理,对能力要求较高.如果合理运用向量法求解,往往会比传统方法更简洁,而且其解题的方法、步骤非常有条理,甚至有一些程式化:建立坐标系→写出点的坐标→求出某些向量的坐标→利用数量积确定点的位置.显然,它不需要很强的推理,只要代入公式,剩下的仅仅是计算,这是使用向量法的优越性所在,也在一定程度上能够弥补部分同学空间想象能力不足的弱点.
例1 如图1,在棱长
为1的正方体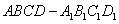 中,P是侧棱 中,P是侧棱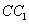 上的一点, 上的一点,
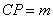 .问在线段 .问在线段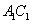 上是否存在一个定点Q,使得对任意的 上是否存在一个定点Q,使得对任意的
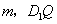 在平面 在平面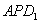 上的射影垂直于AP.并证明你的结论. 上的射影垂直于AP.并证明你的结论.
解:建立如图1所示的空间直角坐标系,则A(1,0,0),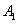 (1,0,1), (1,0,1),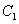 (0,1,1), (0,1,1),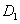 (0,0,1), (0,0,1),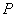 (0,1,m).若在 (0,1,m).若在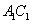 上存在这样的点Q 上存在这样的点Q |

