|
第二章 分式 复习(2)
--------可化为一元一次方程的分式方程
教学目标
1 使学生了解分式方程的概念,进一步掌握分式方程的解法;
2 会列分式方程解应用题.
重点:分式方程的解法和应用
难点:分式方程的应用
教学过程
一 知识要点
做一做:
1解方程:
解:两边同乘以x(x-2),得:5+3(x-2)=x
去分母,得:5+3x-6=x
移项,得: 2x=1
所以,x=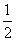
检验:当x=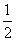 时,x(x-2) 时,x(x-2)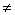 0,所以x= 0,所以x=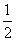 是原方程的解. 是原方程的解.
思考:
1 什么叫分式方程?
分母里含有未知数的方程叫分式方程.
2 解方式方程的思路是什么?有哪些步骤?解分式方程为什么会产生增根?
解分式方程的思路:去分母化为整式方程.
解分式方程的步骤:
(1) 方程两边同乘以最简公分母去掉分母,化为整式方程;
(2) 解整式方程
(3) 检验
(4) 下结论.
解分式方程产生增根的原因:去分母后,方程中未知数的范围扩大了.
2 甲、乙两地相距19千米,某人从甲地去乙地,先步行7千米,然后改骑自行车,共用了两小时到达乙地,已知这个人骑自行车的速度是步行速度的4倍,求步行速度和骑自行车的速度分别是多少?
解:设步行得速度是x千米/时,则骑车的速度是4x/时
依题意得: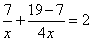
两边同乘以4x,得:28+12=8x
所以,x=5,检验:当x=5时,4x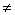 0,所以,x=5是原方程的解.4x=20 0,所以,x=5是原方程的解.4x=20
答:步行速度是5千米/时,骑车的速度是20千米/时.
思考:解分式方程有哪些步骤?
(1) 审题----注意理解题意,抓关键语句.可以借助图表,
(2) 设元-----注意带单位. |

