|
第3课 函数的概念和图象(3)
分层训练
1.一个面积为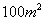 的等腰梯形,上底长为 的等腰梯形,上底长为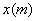 ,下底长为上底长的 ,下底长为上底长的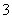 倍,则它的高 倍,则它的高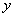 与 与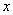 的函数关系是 ( ) 的函数关系是 ( )
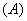 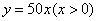 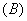 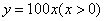
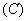 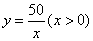 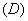 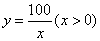
2.下列函数关系中,可以看作二次函数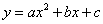 模型的是 ( ) 模型的是 ( )
 在一定距离内,速度与时间的关系 在一定距离内,速度与时间的关系
 若我国人口年自然增长率为 若我国人口年自然增长率为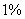 ,则我国人口总数随年份的变化关系 ,则我国人口总数随年份的变化关系
 竖直上抛的物体,从抛起到落回地面时,物体的高度与时间的关系(不计空气阻力) 竖直上抛的物体,从抛起到落回地面时,物体的高度与时间的关系(不计空气阻力)
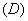 圆周长与半径的关系 圆周长与半径的关系
3.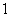 海里约合 海里约合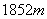 ,根据这一关系,米数 ,根据这一关系,米数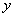 关于海里数 关于海里数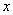 的函数解析式为 的函数解析式为
;
4.用长为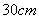 的铁丝围成矩形,将矩形面积 的铁丝围成矩形,将矩形面积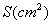 表示为矩形一边长 表示为矩形一边长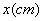 的函数,则函数解析式为 ,函数的定义域为 。 的函数,则函数解析式为 ,函数的定义域为 。
5.物体从静止开始下落,下落的距离与下落时间的平方成正比。已知开始下落的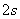 内,物体下落了 内,物体下落了 ,则开始下落的 ,则开始下落的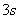 内,物体下落的距离为 。 内,物体下落的距离为 。
6.已知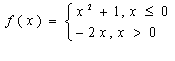 ,若 ,若
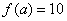 ,则 ,则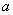 的值为 。 的值为 。
7.某公司将进货单价为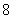 元一个的商品按 元一个的商品按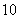 元一个销售,每天可卖出 元一个销售,每天可卖出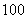 个,已知这种商品的销售单价每上涨一元,销售量就减少 个,已知这种商品的销售单价每上涨一元,销售量就减少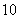 个。 个。
(1)求销售单价为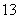 元时的销售利润; 元时的销售利润;
(2)如果销售利润为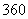 元,那么销售单价上涨了几元? 元,那么销售单价上涨了几元?
8.建造一个容积为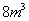 ,深为 ,深为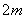 的长方体无盖水池,如果池底和池壁的造价分别为 的长方体无盖水池,如果池底和池壁的造价分别为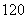 元/ 元/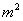 和 和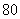 元/ 元/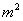 ,求总造价 ,求总造价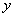 (元)关于底面一边长 (元)关于底面一边长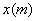 的函数解析式,并指出该函数的定义域。 的函数解析式,并指出该函数的定义域。
拓展延伸
9.某厂生产某种零件,每个零件的成本为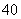 元,出厂单价定为 元,出厂单价定为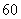 元,该厂为鼓励销售商订购,决定当一次订购量超过 元,该厂为鼓励销售商订购,决定当一次订购量超过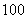 个时,每多订购一个,订购的全部零件的出厂单价就降低 个时,每多订购一个,订购的全部零件的出厂单价就降低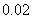 元,但实际出厂单价不能低于 元,但实际出厂单价不能低于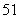 元. 元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为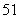 元? 元?
(2)设一次订购量为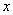 个,零件的实际出厂单价为 个,零件的实际出厂单价为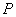 元,写出函数 元,写出函数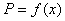 的表达式; 的表达式; (3)当销售商一次订购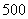 个零件时,该厂获 个零件时,该厂获 |

