|
第10课时线性回归方程(1)
分层训练
1.长方形的面积一定时,长和宽具有( )
(A)不确定性关系 (B)相关关系
(C)函数关系 (D)无任何关系
2.三点(3,10),(7,20),(11,24)的线性回归方程是 ( )
(A) 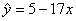 (B) (B) 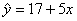 (C) (C)  (D) (D) 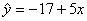
3.已知线性回归方程为: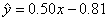 ,则x=25时,y 的估计值为________ ,则x=25时,y 的估计值为________
4.一家保险公司调查其总公司营业部的加班效果,收集了10周中每周加班时间y(小时)与签发新保单数目x的数据如下表:
|
x |
825 |
215 |
1070 |
550 |
480 |
|
y |
3.5 |
1.0 |
4.0 |
2.0 |
1,0 |
|
x |
920 |
1350 |
325 |
670 |
1215 |
|
y |
3.0 |
4.5 |
1.5 |
3.0 |
5.0 |
则y关于x估计的线性回归方程为____________________(保留四位有效数字)
5.炼铝厂测得所产铸模用的铝的硬度x与抗张强度y的数据如下:
|
x |
63 |
53 |
70 |
84 |
60 |
|
y |
288 |
293 |
349 |
343 |
290 |
|
x |
72 |
51 |
83 |
70 |
64 |
|
y |
354 |
283 |
324 |
340 |
286 |
求y与x的线性回归方程。(小数点后保留两位有效数字)
思考 运用 运用
6.在某种产品表面进行腐蚀刻线试验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如下表:
|
x(s) |
5 |
10 |
15 |
20 |
30 |
40 |
|
Y(um) |
6 |
10 |
10 |
13 |
16 |
17 |
|
x(s) |
50 |
60 |
70 |
90 |
120 |
|
|
Y(um) |
19 |
23 |
25 |
29 |
46 |
|
求腐蚀深度y对腐蚀时间x的线性回归方程。
7.假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计资料:
|
使用年限x |
2 |
3 |
4 |
5 |
6 |
|
维修费用y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知y对x呈线性相关关系。
试求:(1)线性回归方程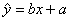 的回归系数 的回归系数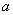 , , 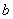 ; ;
(2)估计使用年限为10年时,维修费用是多少?
本节学习疑点:
6.4.1 线性回归方程(1)
1.C 2.D 3.11.69 4.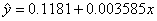
5.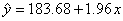
6.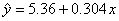
7.(1) 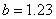 , , 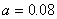
(2) 线性回归方程是 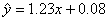
当x=10时,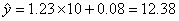
即估计使用10年时的维修费用是12.38万元
|

