|
数列单元练习
1.在等比数列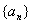 中,若 中,若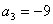 , ,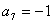 ,则 ,则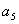 的值为_____________。 的值为_____________。
1.-3.【解析】q4=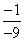 ,q2= ,q2=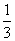 . .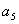 =-9× =-9×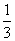 =-3. =-3.
2.在正整数100至500之间能被11整除的个数为 .
2.36.【解析】观察出100至500之间能被11整除的数为110、121、132、…它们构成一个等差数列,公差为11,数an=110+(n-1)·11=11n+99,由an≤500,解得n≤36.
3.在数列{an}中,a1=1,an+1=an2-1(n≥1),则a1+a2+a3+a4+a5等于 。
3.-1.【解析】由已知:an+1=an2-1=(an+1)(an-1),
∴a2=0,a3=-1,a4=0,a5=-1.
4.{an}是等差数列,且a1+a4+a7=45,a2+a5+a8=39,则a3+a6+a9= 。
4.33.【解析】a1+a4+a7,a2+a5+a8,a3+a6+a9成等差数列,故a3+a6+a9=2×39-45=33.
5.正项等比数列{an}中,S2=7,S6=91,则S4= 。
5.28.【解析】∵{an}为等比数列,∴S2,S4-S2,S6-S4也为等比数列,即7,S4-7,91-S4成等比数列,即(S4-7)2=7(91-S4),解得S4=28或-21(舍去).
6.每次用相同体积的清水洗一件衣物,且每次能洗去污垢的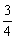 ,若洗n次后,存在的污垢在1%以下,则n的最小值为_________. ,若洗n次后,存在的污垢在1%以下,则n的最小值为_________.
6.4.【解析】每次能洗去污垢的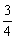 ,就是存留了 ,就是存留了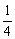 ,故洗n次后,还有原来的( ,故洗n次后,还有原来的(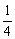 )n,由题意,有:( )n,由题意,有:(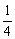 )n<1%,∴4n>100得n的最小值为4. )n<1%,∴4n>100得n的最小值为4.
7.设an=-n2+10n+11,则数列{an}从首项到第几项的和最大是第 项。
7.第10项或11项.【解析】由an=-n2+10n+11=-(n+1)(n-11),得a11=0,而a10>0,a12<0,S10=S11.
8.设函数f(x)满足f(n+1)=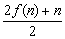 (n∈N*)且f(1)=2,则f(20)= 。 (n∈N*)且f(1)=2,则f(20)= 。
8.97.【解析】f(n+1)-f(n)=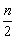 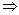 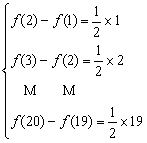
相加得f(20)-f(1)=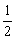 (1+2+…+19) (1+2+…+19)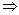 f(20)=95+f(1)=97. f(20)=95+f(1)=97.
9.某大楼有20层,有19人在第一层上了电梯,他们分别要去第2层到20层,每层一人,而电梯只允许停一次,可只使一人满意,其余18人都要上楼或下楼。假设乘客每向下走一层不满意度为1,每向上走一层不满意度为2。所有人不满意之和为S,为使S最小,电梯应停在第 层。
9.14.【解析】设停在第k层,不满意度为S=1+2+…+(k-2)+2(1+2+3+..+20-k) =
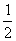 (3k2-85k+842),k=14时S最小。 (3k2-85k+842),k=14时S最小。
10.等比数列{an},an>0,q≠1,且a2、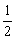 a3、a1成等差数列,则 a3、a1成等差数列,则 = 。 = 。
10.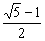 . 【解析】依题意:a3=a1+a2,则有a1q2=a1+a1q,∵a1>0,∴q2=1+q . 【解析】依题意:a3=a1+a2,则有a1q2=a1+a1q,∵a1>0,∴q2=1+q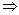 q= q=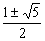 . . 又∵an>0.∴q>0,∴q=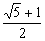 , , |

