|
22.2 二次根式的乘除法(3)
第三课时
教学内容
最简二次根式的概念及利用最简二次根式的概念进行二次根式的化简运算.
教学目标
理解最简二次根式的概念,并运用它把不是最简二次根式的化成最简二次根式.
通过计算或化简的结果来提炼出最简二次根式的概念,并根据它的特点来检验最后结果是否满足最简二次根式的要求.
重难点关键
1.重点:最简二次根式的运用.
2.难点关键:会判断这个二次根式是否是最简二次根式.
教学方法 三疑三探
教学过程
一、设疑自探——解疑合探
自探1.(学生活动)请同学们完成下列各题(请三位同学上台板书)
计算(1)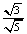 ,(2) ,(2)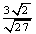 ,(3) ,(3)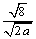
老师点评: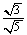 = =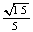 , ,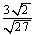 = =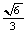 , ,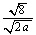 = =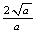
自探2. 观察上面计算题的最后结果,可以发现这些式子中的二次根式有什么特点?(有如下两个特点:1.被开方数不含分母; 2.被开方数中不含能开得尽方的因数或因式.)
我们把满足上述两个条件的二次根式,叫做最简二次根式.
合探1.把下面的二次根式化为最简二次根式:
(1) 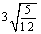 ; (2) ; (2)  ; (3) ; (3) 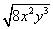
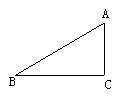 合探2.如图,在Rt△ABC中,∠C=90°,AC=2.5cm,BC=6cm,求AB的长. AB= 合探2.如图,在Rt△ABC中,∠C=90°,AC=2.5cm,BC=6cm,求AB的长. AB=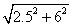 = =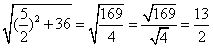 =6.5(cm) =6.5(cm)
|

