|
第2课时 函数的定义域和值域
一、定义域:
1.函数的定义域就是使函数式 的集合.
2.常见的三种题型确定定义域:
① 已知函数的解析式,就是 .
② 复合函数f [g(x)]的有关定义域,就要保证内函数g(x)的 域是外函数f (x)的 域.
③实际应用问题的定义域,就是要使得 有意义的自变量的取值集合.
二、值域:
1.函数y=f (x)中,与自变量x的值 的集合.
2.常见函数的值域求法,就是优先考虑 ,取决于 ,常用的方法有:①观察法;②配方法;③反函数法;④不等式法;⑤单调性法;⑥数形法;⑦判别式法;⑧有界性法;⑨换元法(又分为 法和 法)
例如:① 形如y=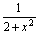 ,可采用 法;② y= ,可采用 法;② y=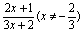 ,可采用 法或 法;③ y=a[f (x)]2+bf (x)+c,可采用 法;④ y=x- ,可采用 法或 法;③ y=a[f (x)]2+bf (x)+c,可采用 法;④ y=x-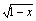 ,可采用 法;⑤ y=x- ,可采用 法;⑤ y=x-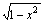 ,可采用 法;⑥ y= ,可采用 法;⑥ y=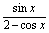 可采用 法等. 可采用 法等.
例1. 求下列函数的定义域:
(1)y= ; (2)y= ; (2)y=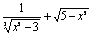 ; (3)y= ; (3)y=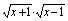 . .
解:(1)由题意得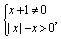 化简得 化简得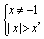
即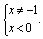 故函数的定义域为{x|x<0且x≠-1}. 故函数的定义域为{x|x<0且x≠-1}.
(2)由题意可得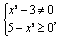 解得 解得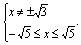 故函数的定义域为{x|-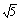 ≤x≤ ≤x≤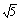 且x≠± 且x≠± |

