|
§1.3.1函数的最大(小)值
一.教学目标
1.知识与技能:
理解函数的最大(小)值及其几何意义.
学会运用函数图象理解和研究函数的性质.
2.过程与方法:
通过实例,使学生体会到函数的最大(小)值,实际上是函数图象的最高(低)点的纵坐标,因而借助函数图象的直观性可得出函数的最值,有利于培养以形识数的解题意识.
3.情态与价值
利用函数的单调性和图象求函数的最大(小)值,解决日常生活中的实际问题,激发学生学习的积极性.
二.教学重点和难点
教学重点:函数的最大(小)值及其几何意义
教学难点:利用函数的单调性求函数的最大(小)值.
三.学法与教学用具
1.学法:学生通过画图、观察、思考、讨论,从而归纳出求函数的最大(小)值的方法和步骤.
2.教学用具:多媒体手段
四.教学思路
(一)创设情景,揭示课题.
画出下列函数的图象,指出图象的最高点或最低点,并说明它能体现函数的什么特征?
①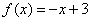 ② ②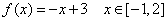
③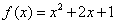 ④ ④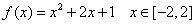
(二)研探新知
1.函数最大(小)值定义
最大值:一般地,设函数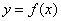 的定义域为I,如果存在实数M满足: 的定义域为I,如果存在实数M满足:
(1)对于任意的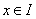 ,都有 ,都有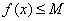 ; ;
(2)存在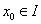 ,使得 ,使得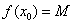 . . 那么,称M是函数 |

