|
第4课时 函数的奇偶性
1.奇偶性:
① 定义:如果对于函数f (x)定义域内的任意x都有 ,则称f (x)为奇函数;若 ,则称f (x)为偶函数. 如果函数f (x)不具有上述性质,则f (x)不具有 . 如果函数同时具有上述两条性质,则f (x) .
② 简单性质:
1) 图象的对称性质:一个函数是奇函数的充要条件是它的图象关于 对称;一个函数是偶函数的充要条件是它的图象关于 对称.
2) 函数f(x)具有奇偶性的必要条件是其定义域关于 对称.
2.与函数周期有关的结论:
①已知条件中如果出现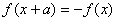 、或 、或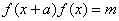 ( (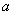 、 、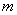 均为非零常数, 均为非零常数,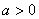 ),都可以得出 ),都可以得出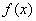 的周期为 ; 的周期为 ;
②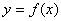 的图象关于点 的图象关于点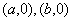 中心对称或 中心对称或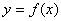 的图象关于直线 的图象关于直线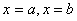 轴对称,均可以得到 轴对称,均可以得到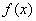 周期 周期
例1. 判断下列函数的奇偶性.
(1)f(x)=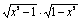 ; ;
(2)f(x)=log2(x+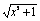 ) (x∈R); ) (x∈R);
(3)f(x)=lg|x-2|.
解:(1)∵x2-1≥0且1-x2≥0,∴x=±1,即f(x)的定义域是{-1,1}.
∵f(1)=0,f(-1)=0,∴f(1)=f(-1),f(-1)=-f(1),
故f(x)既是奇函数又是偶函数.
(2)方法一 易知f(x)的定义域为R,
又∵f(-x)=log2[-x+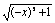 ]=log2 ]=log2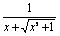 =-log2(x+ =-log2(x+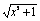 )=-f(x), )=-f(x),
∴f(x)是奇函数. |

