|
第9课时 函数与方程
1.一元二次函数与一元二次方程
一元二次函数与一元二次方程(以后还将学习一元二次不等式)的关系一直是高中数学函数这部分内容中的重点,也是高考必考的知识点.我们要弄清楚它们之间的对应关系:一元二次函数的图象与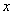 轴的交点的横坐标是对应一元二次方程的解;反之,一元二次方程的解也是对应的一元二次函数的图象与 轴的交点的横坐标是对应一元二次方程的解;反之,一元二次方程的解也是对应的一元二次函数的图象与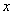 轴的交点的横坐标. 轴的交点的横坐标.
2.函数与方程
两个函数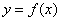 与 与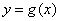 图象交点的横坐标就是方程 图象交点的横坐标就是方程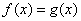 的解;反之,要求方程 的解;反之,要求方程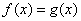 的解,也只要求函数 的解,也只要求函数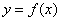 与 与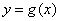 图象交点的横坐标. 图象交点的横坐标.
3.二分法求方程的近似解
二分法求方程的近似解,首先要找到方程的根所在的区间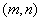 ,则必有 ,则必有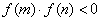 ,再取区间的中点 ,再取区间的中点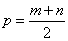 ,再判断 ,再判断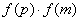 的正负号,若 的正负号,若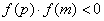 ,则根在区间 ,则根在区间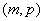 中;若 中;若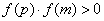 ,则根在 ,则根在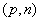 中;若 中;若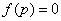 ,则 ,则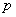 即为方程的根.按照以上方法重复进行下去,直到区间的两个端点的近似值相同(且都符合精确度要求),即可得一个近似值. 即为方程的根.按照以上方法重复进行下去,直到区间的两个端点的近似值相同(且都符合精确度要求),即可得一个近似值.
例1.(1)若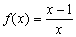 ,则方程 ,则方程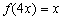 的根是( ) 的根是( )
A.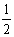 B.- B.-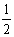 C.2 D.-2 C.2 D.-2
解:A.
(2)设函数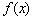 对 对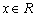 都满足 都满足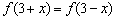 ,且方程 ,且方程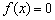 恰有6个不同的实数根,则这6个实根的和为( ) 恰有6个不同的实数根,则这6个实根的和为( )
A.0 B.9 C.12 D.18
解:由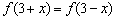 知 知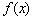 的图象有对称轴 的图象有对称轴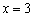 ,方程 ,方程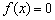 的6个根在 的6个根在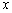 轴上对应的点关于直线 轴上对应的点关于直线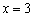 对称,依次设为 对称,依次设为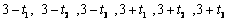 ,故6个根的和为18,答案为D. ,故6个根的和为18,答案为D.
|

