|
复习引入 |
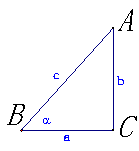 1.在初中我们学习了锐角三角函数,它是以锐角为自变量,边的比值为函数值的三角函数: 1.在初中我们学习了锐角三角函数,它是以锐角为自变量,边的比值为函数值的三角函数:
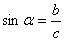 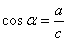
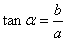 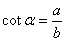
|
教师提出问题:初中是如何定义角的?
师:前面我们对角的概念进行了扩充,并学习了弧度制,知道角的集合与实数集是一一对应的,在这个基础上,今天我们来研究任意角的三角函数. |
温故知新 |
|
概念形成 |
1.用坐标形式表示出中所学的锐角三角函数
设点P(x,y)是锐角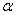 终边上的任意一点,记OP=r(r≠0), 终边上的任意一点,记OP=r(r≠0),
则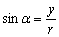 , ,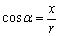 , ,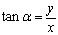
2.任意角的三角函数
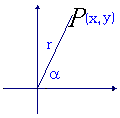 设 设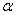 是一个任意角,在 是一个任意角,在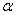 的终边上任取(异于原点的)一点P(x,y) 的终边上任取(异于原点的)一点P(x,y)
则P与原点的距离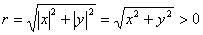  根据三角形的相似知识得到 根据三角形的相似知识得到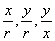 均为定值。 均为定值。
比值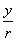 叫做 叫做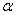 的正弦, 的正弦,
记作: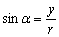
比值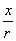 叫做 叫做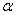 的余弦, 的余弦,
记作: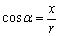
比值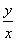 叫做 叫做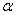 的正切, 的正切,
记作: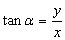
(4)角的其它三种三角函数
比值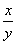 叫做 叫做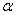 的余切, 的余切,
记作: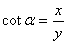
比值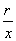 叫做 叫做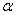 的正割, 的正割,
记作: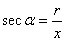
比值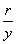 叫做 叫做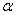 的余割, 的余割,
记作: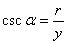
|
1. 以坐标原点为锐角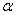 的顶点,以Ox轴为角 的顶点,以Ox轴为角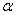 的始边,则角 的始边,则角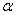 的终边落在直角坐标系的第一象限内,若设点P(x,y)始终边上的任意一点,记OP=r(r≠0),试将角 的终边落在直角坐标系的第一象限内,若设点P(x,y)始终边上的任意一点,记OP=r(r≠0),试将角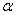 的三角函数用x,y,y表示出来. 的三角函数用x,y,y表示出来.
学生作图,教师在此过程中要引导学生在坐标系中做出符合锐角三角函数定义要求的直角三角形.该过程中要适时指点学生,并加强学生与学生之间的讨论与交流.
回答问题:教师通过多媒体将此过程展示给学生,明确坐标与三角函数的关系.
2. 教师提出问题:
问题1:根据刚才我们在直角坐标系中讨论的锐角三角函数,你能给出任意角的三角函数定义吗?
由学生讨论回答.
问题2: 角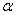 的三角函数值不受终边上的点P的位置的影响吗? 的三角函数值不受终边上的点P的位置的影响吗?
这是一个较有思考价值的问题,教师要注意正确地引导和必要地提示,锐角三角函数的大小仅与锐角的大小有关,与直角三角形的大小无关,类似地-…
问题3: 依据函数的定义,这几个比值可以分别构成函数吗?若能构成,他们的自变量是什么?x还是y?r还是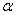 ? ?
|
将初中定义的锐角三角函数放到坐标系中的讨论,指明研究函数问题的工具,完成从三角形到坐标系的转化,为后面在直角坐标系中定义任意角的三角函数搭建平台。
2.通过对比,让学生对知识进行类比、迁移及联想,树立他们勇于探索的信心。通过讨论,充分发挥学生学习的主动性 |

