|
教学内容: §2.3平面向量的基本定理及坐标表示(1)
|
教学目标 |
1.理解平面向量的基本定理,会作出由已知一组基底所表示的向量;
2.理解向量夹角及垂直的概念;
3.理解向量的正交分解,感受正交分解的实际意义,掌握向量的坐标表示。 |
|
本节重点 |
平面向量的基本定理,向量的正交分解及坐标表示 |
|
本节难点 |
平面向量的基本定理 |
|
教学模式 |
|
|
教学过程 |
主 要 内 容 及 板 书 |
|
摘要与反思
|
一.复习旧知,设问引入
1.设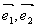 是不共线的向量,而 是不共线的向量,而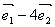 , ,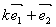 共线,则实数 共线,则实数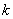 = . = .
2.思考(P103思考)给定平面内任意两个向量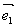 、 、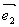 ,请你作出向量 ,请你作出向量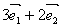 、 、
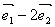 。平面内的任一向量是否都可以用形如 。平面内的任一向量是否都可以用形如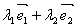 的向量表示呢? 的向量表示呢?
二.探究新课
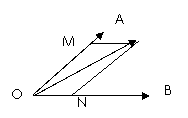 1.在黑板上画出两个不共线的向量 1.在黑板上画出两个不共线的向量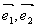 及任一向量 及任一向量 ,如图,请学生回答:能否用向量 ,如图,请学生回答:能否用向量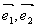 表示向量 表示向量 ?如何表示? ?如何表示?
在平面内任取一点O,作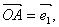 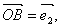 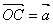 .过C作平行于直线OB的直线,与直线OA交于M;过点C作平行于直线OA的直线,与直线OB交于N.则有且只有实数 .过C作平行于直线OB的直线,与直线OA交于M;过点C作平行于直线OA的直线,与直线OB交于N.则有且只有实数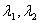 ,使得 ,使得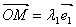 , ,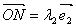 ,所以 ,所以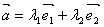 ,也就是说,任一向量 ,也就是说,任一向量 ,可以表示成 ,可以表示成 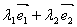 的形式.并且可以证明 的形式.并且可以证明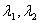 是唯一的. 是唯一的.
2.平面向量基本定理:如果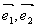 是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量 是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量 ,有且只有一对实数 ,有且只有一对实数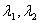 ,使 ,使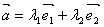 . . | |

