|
第3课时 平面向量的数量积
1.两个向量的夹角:已知两个非零向量 和 和 ,过O点作 ,过O点作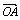 = = , ,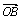 = = ,则∠AOB=θ (0°≤θ≤180°) 叫做向量 ,则∠AOB=θ (0°≤θ≤180°) 叫做向量 与 与 的 .当θ=0°时, 的 .当θ=0°时, 与 与 ;当θ=180°时, ;当θ=180°时, 与 与 ;如果 ;如果 与 与 的夹角是90°,我们说 的夹角是90°,我们说 与 与 垂直,记作 . 垂直,记作 .
2.两个向量的数量积的定义:已知两个非零向量 与 与 ,它们的夹角为θ,则数量 叫做 ,它们的夹角为θ,则数量 叫做 与 与 的数量积(或内积),记作 的数量积(或内积),记作 · · ,即 ,即 · · = .规定零向量与任一向量的数量积为0.若 = .规定零向量与任一向量的数量积为0.若 =(x1, y1), =(x1, y1), =(x2, y2),则 =(x2, y2),则 · · = . = .
3.向量的数量积的几何意义:
| |cosθ叫做向量 |cosθ叫做向量 在 在 方向上的投影 (θ是向量 方向上的投影 (θ是向量 与 与 的夹角). 的夹角).
 · · 的几何意义是,数量 的几何意义是,数量 · · 等于 . 等于 .
4.向量数量积的性质:设 、 、 都是非零向量, 都是非零向量,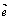 是单位向量,θ是 是单位向量,θ是 与 与 的夹角. 的夹角.
⑴ 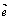 · · = = · ·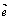 = =
⑵  ⊥ ⊥ 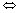
⑶ 当 与 与 同向时, 同向时, · · = ;当 = ;当 与 与 反向时, 反向时, · · = . = .
⑷ cosθ= .
⑸ | · · |≤ |≤ |

