|
一.课题:集合的运算
二.教学目标:理解交集、并集、全集、补集的概念,掌握集合的运算性质,能利用数轴或文氏图进行集合的运算,进一步掌握集合问题的常规处理方法.
三.教学重点:交集、并集、补集的求法,集合语言、集合思想的运用.
四.教学过程:
(一)主要知识:
1.交集、并集、全集、补集的概念;
2.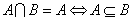 , ,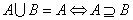 ; ;
3.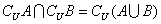 , ,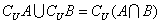 . .
(二)主要方法:
1.求交集、并集、补集,要充分发挥数轴或文氏图的作用;
2.含参数的问题,要有讨论的意识,分类讨论时要防止在空集上出问题;
3.集合的化简是实施运算的前提,等价转化常是顺利解题的关键.
(三)例题分析:
例1.设全集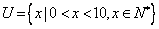 ,若 ,若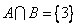 , ,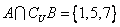 , , ,则 ,则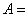  , ,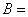 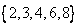 . .
解法要点:利用文氏图.
例2.已知集合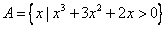 , ,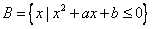 ,若 ,若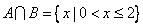 , ,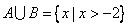 ,求实数 ,求实数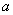 、 、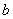 的值. 的值.
解:由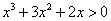 得 得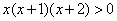 ,∴ ,∴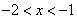 或 或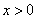 , ,
∴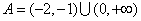 ,又∵ ,又∵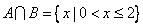 ,且 ,且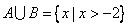 , ,
∴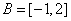 ,∴ ,∴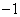 和 和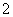 是方程 是方程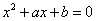 的根, 的根,
由韦达定理得: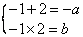 ,∴ ,∴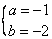 . .
说明:区间的交、并、补问题,要重视数轴的运用.
例3.已知集合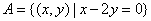 , ,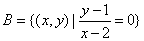 ,则 ,则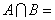  ; ;
 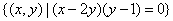 ;(参见《高考 ;(参见《高考 计划》考点2“智能训练”第6题). 计划》考点2“智能训练”第6题).
解法要点:作图.
注意:化简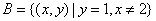 , ,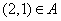 . . |

