|
2.1.1 函数 学案(1)
【预习要点及要求】
1.理解函数的概念;
2.会用集合与对应语言来刻画函数,了解构成函数的要素.
【知识再现】在初中,已学习了变是与函数的概念,在一个变化过程中有两个变量x和y,如果给定一个x值,相应地就确定唯一的一个y值,那么我们就称y是x的函数,其中x是自变量,y是因变量.
【概念探究】
自学课本P29—P31,填充以下空格.
1、设集合A是一个非空的实数集,对于A内 ,按照确定的对应法则f,都有 与它对应,则这种对应关系叫做集合A上的一个函数,记作 .
2、对函数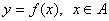 ,其中x叫做 ,x的取值范围(数值A)叫做这个函数的 ,所有函数值的集合 ,其中x叫做 ,x的取值范围(数值A)叫做这个函数的 ,所有函数值的集合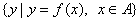 叫做这个函数的 ,函数y=f(x) 也经常写为 . 叫做这个函数的 ,函数y=f(x) 也经常写为 .
3、因为函数的值域被 完全确定,所以确定一个函数只需要
.
4、依函数定义,要检验两个给定的变量之间是否存在函数关系,只要检验:①
;② .
5、设a, b是两个实数,且a
(1)满足不等式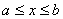 的实数x的集合叫做闭区间,记作 . 的实数x的集合叫做闭区间,记作 .
(2)满足不等式a的实数x的集合叫做开区间,记作 .
(3)满足不等式 或 或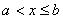 的实数x的集合叫做半开半闭区间,分别表示为 的实数x的集合叫做半开半闭区间,分别表示为
,其中实数a, b表示区间的两端点.
完成课本P33,练习A 1、2;练习B 1、2、3.
【总结点拨】
函数的映射定义与传统定义在实质上是一致的,两个定义中的定义域和值域完全相同对应法则也一样,只不过叙述的出发点不同,传统定义是从运动变化的观点出发,近代定义从集合与对应的观点出发,为下一节做准备.
【例题讲解】
例1.求函数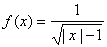 的定义域. 的定义域.
|

