|
3.1.1两角和与差的余弦(二)
(一) 教学目标
1、知识目标:会用公式求值和证明。
2、能力目标:培养学生分析问题解决问题的能力,推理,联想能力。
3、情感目标:发展学生的正向,逆向思维能力,前后知识灌溉和呼应的能力,培养良好、严谨的数学思维品质。
(二) 教学重点,难点
重点是运用公式求值,证明,并建立与原有知识(诱导公式),方法(旋转变换)的联系。
难点是公式的变形和逆向应用。
(三) 教学方法
教师按照例题设计的思路适度引导学生自发地思考问题,通过提问,讨论等形式来促使学生自己思考,自发学习,获得解决问题的途径,同时构建基于旧有知识的更新结构体系。同时,通过切身的尝试和参与来实现思维能力的提升,以达到对这一公式熟练掌握和灵活运用的目的。
(四) 教学过程
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
|
复
习
引
入 |
复习公式
|
让学生默写两角和与差的余弦公式。同时,从公式形式出发,让学生总结提炼该公式的本质思想:讨论角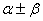 的余弦和单角 的余弦和单角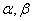 的正弦,余弦函数间的关系,于是,利用这一公式我们可以用已知特殊角来求得某些角的余弦。 的正弦,余弦函数间的关系,于是,利用这一公式我们可以用已知特殊角来求得某些角的余弦。 |
温习所学,引导学生积极思考,进而由简渐繁,强化应用。
|
|
设置例题,
复习强化 |
P135 A,
2 (2)(3)
|
学生练习,板演,教师讲评。
|
是对公式的简单应用。在第二个问题的处理上要用到诱导公式。也是为下一步工作的开展做铺垫。 |
|
形式出发,小作提升 |
教材例2。
分析,解决完此问题之后,通过练习B中题目2来巩固该方法和步骤。
|
思考:
由公式形式来看,对其应用是不是仅仅局限于特殊角?
由对公式的理解我们知道:由公式出发,比特殊角更广泛的角可以加入进来。前提是只要知道其正,余弦值。
看教材中的例2。
提问:
欲求其值,打算用何工具?
题目中是否具有了该工具可行的条件?
该条件能否实现?如能,怎么实现?
通过学生讨论,找到解决问题的办法——利用和角余弦公式,通过判断各象限角的正,余弦的符号这一部分内容完成题目的瓶颈问题。再利用公式得结果。 |
在以上过程中感受解决此类问题的思想,步骤。进一步,通过学生对练习B中题目2的练习达到巩固这一类问题的目的。
| |

