|
用构造法求数列的通项公式
求数列的通项公式是高考重点考查的内容,作为两类特殊数列 ----等差数列·等比数列可直接 ----等差数列·等比数列可直接 根据它们的通项公式求解,但也有一些数列要通过构造转化为等差数列或等比数列,之后再应用各自的通项公式求解,体现化归思想在数列中的具体应用 根据它们的通项公式求解,但也有一些数列要通过构造转化为等差数列或等比数列,之后再应用各自的通项公式求解,体现化归思想在数列中的具体应用
例1:(06年福建高考题)数列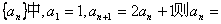 ( ) ( )
A.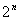  B. B.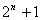 C. C.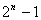 D. D. 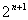 [来源:学&科&网] [来源:学&科&网]
解法1: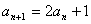
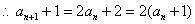
又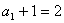
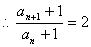
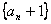 是首项为2公比 是首项为2公比 为2的等比数列[来源:Zxxk.Com][来源:学科网ZXXK][来源:Zxxk.Com] 为2的等比数列[来源:Zxxk.Com][来源:学科网ZXXK][来源:Zxxk.Com]
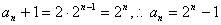 ,所以选C ,所以选C
解法2[来源:Z#xx#k.Com][来源:学,科,网Z,X,X,K]
[来源:Z_xx_k.Com]
归纳总结:若数列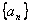 满足 满足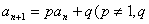 为常数),则令 为常数),则令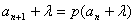 来构造等比数列,并利用 来构造等比数列,并利用 对应项相等求 对应项相等求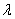 的值,求通项公式。 的值,求通项公式。
例2:数列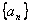 中, 中,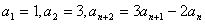 ,则 ,则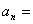 。 。
解: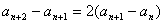
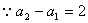   为首项为2公比也为2的等比数列。 为首项为2公比也为2的等比数列。
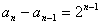 ,( ,( n> n> |

