|
数学归纳法解题
数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应用的一种主要思想方法.
●难点磁场
(★★★★)是否存在a、b、c使得等式1·22+2·32+…+n(n+1)2=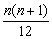 (an2+bn+c). (an2+bn+c).
●案例探究
[例1]试证明:不论正数a、b、c是等差数列还是等比数列,当n>1,n∈N*且a、b、c互不相等时,均有:an+cn>2bn.
命题意图:本题主要考查数学归纳法证明不等式,属★★★★级题目.
知识依托:等差数列、等比数列的性质及数学归纳法证明不等式的一般步骤.
错解分析:应分别证明不等式对等比数列或等差数列均成立,不应只证明一种情况.
技巧与方法:本题中使用到结论:(ak-ck)(a-c)>0恒成立(a、b、c为正数),从而ak+1+ck+1>ak·c+ck·a.
证明:(1)设a、b、c为等比数列,a=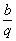 ,c=bq(q>0且q≠1) ,c=bq(q>0且q≠1)
∴an+cn=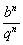 +bnqn=bn( +bnqn=bn(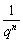 +qn)>2bn +qn)>2bn
(2)设a、b、c为等差数列,则2b=a+c猜想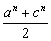 >( >(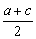 )n(n≥2且n∈N*) )n(n≥2且n∈N*)
下面用数学归纳法证明:
①当n=2时,由2(a2+c2)>(a+c)2,∴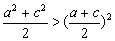
②设n=k时成立,即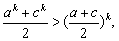
则当n=k+1时,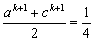 (ak+1+ck+1+ak+1+ck+1) (ak+1+ck+1+ak+1+ck+1)
>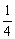 (ak+1+ck+1+ak·c+ck·a)= (ak+1+ck+1+ak·c+ck·a)=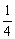 (ak+ck)(a+c) (ak+ck)(a+c)
>(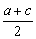 )k·( )k·(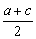 )=( )=(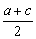 )k+1 )k+1
[例2]在数列{an}中,a1=1,当n≥2时,an,Sn,Sn-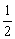 成等比数列. 成等比数列. (1)求 |

