|
课题:无穷等比数列各项的和(第一课时)
[教学目标]
1、掌握无穷等比数列各项的和的定义及公式的推导;
2、理解无数个数的和与有限个数的和在意义上的区别;
3、在利用等比数列各项和的公式解决一些简单的实际问题过程中,培养和提高数学的应用意识。
[教学重点]
1、 等比数列各项和的定义及公式的推导;
2、 等比数列各项和在一些简单的实际问题中的应用。
[教学难点]
正确理解无穷等比数列各项和的定义
[教学过程]
|
教师活动 |
学生活动 |
点评 |
|
一、新课引入
问题: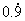 和1哪个数大?为什么? 和1哪个数大?为什么?
为解决这一问题,可以引导学生回答以下问题:
1、 如果你认为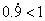 ,那么 ,那么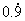 比1小多少? 比1小多少?
2、 如果你认为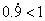 ,那么你能否找到一个实数a,使得 ,那么你能否找到一个实数a,使得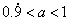 成立? 成立?
3、 有同学这样思考:
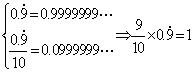
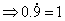
他的说法正确吗?你能否利用现有的数学知识来解释一下?
4:有同学利用极限的思想来解释了为什么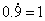 。我们能否换一个角度来看一下呢?事实上 。我们能否换一个角度来看一下呢?事实上
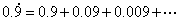
你能否作出合理的解释。 |
学生以小组为单位进行讨论,然后展示他们的结果。
(大部分学生会回答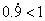 ,部分学生知道 ,部分学生知道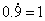 但无法说明理由。针对这一现象教师通过一系列问题的设计引导学生逐步认识到 但无法说明理由。针对这一现象教师通过一系列问题的设计引导学生逐步认识到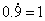 的原因。) 的原因。)
对于问1,估计学生会回答: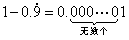 。教师应该引导学生认识到 。教师应该引导学生认识到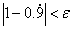 ,即 ,即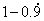 得极限为0。 得极限为0。
对于问2,引导学生认识到不存在满足条件的实数a,由实数的稠密性可以说明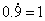
对于问3,进一步让学生明确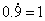 是正确的,从而引导学生思考为什么在一开始会出错。 是正确的,从而引导学生思考为什么在一开始会出错。
估计,此时会有学生构造数列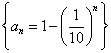 ,学生会认为 ,学生会认为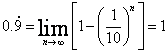 。此时,学生将 。此时,学生将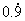 和极限联系在一起,教师因引导学生从另外一个角度看问题。 和极限联系在一起,教师因引导学生从另外一个角度看问题。 |
| |

