课题:无穷等比数列各项的和（1）

课标要求:会求无穷等比数列各项的和。

教学目标：

1、            理解无穷等比数列各项和的含义，掌握无穷等比数列各项和的公式，会求无穷等比数列各项的和；

2、            会用无穷等比数列各项和解决相关问题；

3、            体会用极限的思想来解决无穷等比数列的求和问题，感悟用有限来刻画无限，深刻体会有限和无限的区别和联系；

4、            通过等比数列各项和的探究过程培养学生的探究意识以及提高数学的应用意识和能力。

教学重点:

1、            等比数列各项和的定义及公式的推导；

2、            等比数列各项和在一些简单的实际问题中的应用。

教学难点:正确理解无穷等比数列各项和的定义。

教学过程：

一、新课引入

1、引例1:有理数运算: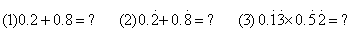

2、引例2: 由于空气的阻力，因此某一类钟的钟摆每摆动一次的弧的长度都是其上一次摆动弧的长度的95%，假设其第一次摆动弧的长度为40cm，求它在停止前所有摆动的弧的长度和。(请用一个式子来表示求解的问题)

3、点题：无穷等比数列各项和

二、概念形成

4、温故:无穷等比数列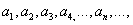

通项公式: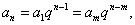