|
第十二章 圆锥曲线
一、轨迹方程
1、求轨迹方程的几个步骤:(建-设-列-化-证)
a.建系(建立平面直角坐标系,多数情况此步省略)
b.设点(求哪个点的轨迹,就设它(x,y))
c.列式(根据条件列等量关系)
d.化简(化到可以看出轨迹的种类)
e.证明(改成:修正)(特别是①三角形、②斜率、③弦的中点问题)
2、求动点轨迹方程的几种方法
a.直接法:题目怎么说,列式怎么列。
b.定义法:先得到轨迹名称
c.代入法(相关点法):设所求点(x,y)另外点(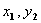 )找出已知点和所求点的关系 )找出已知点和所求点的关系
c.参数法:(x,y)中x,y都随另一个量变化而变化—消参
二、弦长
若直线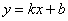 与二次曲线的交点为A( 与二次曲线的交点为A(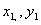 )和B ( )和B (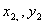 ) )
方法一:联立直线与二次曲线方程求出两交点 两点间距离 两点间距离
方法二:利用弦长公式: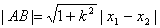 = =
 = =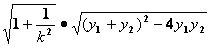
方法三:(半弦长)2=(半径)2-(圆心到直线距离)2(—只适用于圆)
三、直线与二次曲线交点
|
公共点个数 |
两个 |
一个 |
无 |
|
 法(代数法)(注意二次项系数的讨论) 法(代数法)(注意二次项系数的讨论)
|
 >0 >0
|
 =0 =0
|
 <0 <0
|
|
d与r(几何法)(--只适用与圆) |
d |
d=r |
d>r |
四、弦的中点问题
方法一:利用圆的圆心与弦中点的连线与弦垂直。(—只适用于圆)
方法二:点差法—不能用于判别存在性问题。
方法三:联立方程后利用两根之和与中点的关系—求存在性问题或求范围时需考虑 。 。
五、椭圆
1.另椭圆还具有以下性质
a.椭圆上到中心的距离最小的点是短轴的两个端点,最大的点是长轴的两个端点;
b.椭圆上到焦点距离最大、最小的点是长轴的两个端点(天体运动中称“远日点”“近日点”) 最大、最小距离分别为a+c, a-c; c.设椭圆的两个焦点F1、F2当椭 |

