|
v
课题:3.3函数的运算
一、 教学内容分析
函数的运算内容较为简单,关键在于求和(积)函数的定义域,但其重要性却不容忽视,首先,函数的运算体现了高中数学的一大基本思想方法----转化思想,把陌生化为熟悉,把复 杂的函数看作简单的函数的和(积)。其次,由函 杂的函数看作简单的函数的和(积)。其次,由函 数的运算引出 数的运算引出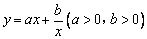 的图像,利用此类 的图像,利用此类 函数的单调性可以解决许多最值问题。[来源:Z.xx.k.Com] 函数的单调性可以解决许多最值问题。[来源:Z.xx.k.Com]
为了引入函数运算,我从实例出发构造了利用基本不等式所不能解决的一个求最值的问题,这样通过创设问题情景,突出了函数运算的必要性,增强学生解决问题的内驱力。最后运用函数运算,画出耐克函数,解决实例所提出的最值问题。
二、教学目标设计
1.理解函数运算的概念及简单的应用。
2.通过 对例题的讲解,让学生体会到数形结合,转化思想的重要性。[来源:学+科+网] 对例题的讲解,让学生体会到数形结合,转化思想的重要性。[来源:学+科+网]
三 、教学重点及难点[来源:Zxxk.Com] 、教学重点及难点[来源:Zxxk.Com]
函数运算的定义;
函数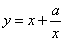 ( a ( a > 0 ) 图像画法及性质分析。 > 0 ) 图像画法及性质分析。
四、教 学过程设计 学过程设计
1、引入函数运算
问题1:甲,乙两实验室相距1千米,开车从甲匀速 到乙实验室,速度为 到乙实验室,速度为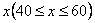 千米/小时。已知小车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可变部分与速度 千米/小时。已知小车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可变部分与速度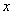 (千米/小时)的平方成正比,比例系数为1,固定部分为2元[来源:Z+xx+k.Com] (千米/小时)的平方成正比,比例系数为1,固定部分为2元[来源:Z+xx+k.Com]
1)把全程运 输成本 输成本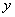 表示为速度 表示为速度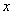 的函数。 的函数。
 2)为了使全程运输成本最小,汽车应以多大速度行驶。 2)为了使全程运输成本最小,汽车应以多大速度行驶。
怎样求最小成本?能否用基本不等式求最小成本?
另找途径。观察此函数与我们所熟悉的那些函数有关?有何关系? |

