|
等差数列前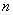 项和(一) 项和(一)
教学目标:
1.掌握等差数列前n项和公式及其获取思路.
2.会用等差数列的前n项和公式解决一些简单的与前n项和有关的问题.
教学重难点:
1.教学重点: 等差数列n项和公式的理解、推导.
2.教学难点:获得等差数列前n项和公式推导的思路.
一、课前预习:
阅读教材:P15---P18
1. 等差数列 求和公式__________________;推导方法:___________ 求和公式__________________;推导方法:___________
自主测评:
1. [等差数列 的前 的前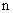 项和为 项和为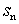 ,若 ,若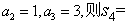 ( ) ( )
(A)12 (B)10 (C)8 (D)6
2.等差数列 { a n } 中 ,a 1 = 1 , a 3 + a 5 = 14,其前n项和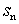 = 100 , 则n =( ) = 100 , 则n =( )
(A) 9 (B) 10 (C) 11 (D) 12
3.等差数列 中, 中, ,那么a 1 + a 10 = ,那么a 1 + a 10 =
4.著名的数学家 高斯(德国 1777-1855 )十岁时计算 : 1+2+3+…+100的故事归结为 1.这是求等差数列1,2,3,…,100前100项和,高 )十岁时计算 : 1+2+3+…+100的故事归结为 1.这是求等差数列1,2,3,…,100前100项和,高  斯的解法是:___________. 斯的解法是:___________.
二、教学过程
复习回顾: 在等差数列中:(:11 )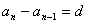 (n≥1) (n≥1) , ,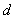 为常数[来源:Z。xx。k.Com] 为常数[来源:Z。xx。k.Com] ( 2)若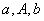 为等 为等 |

