|
§2.1 等差数列(二)
宜黄县安石中学 万 杰
教学目标
1.知识与技能:能在具体的问题情境中,发现数列的等差关系并能用有关知识解决相应的问题;体会等差数列与一次函数的关系。
2. 过程与方法:进行等差数列通项公式应用的实践操作并在操作过程中,通过类比函数概念、性质、表达式得到对等差数列相应问题的研究。
3.情态与价值:培养学生观察、归纳的能力,培养学生的应用意识。
教学重点:会用公式解决一些简单的问题,体会等差数列与一次函数之间的联系。
教学难点:等差数列与一次函数之间的联系
教学过程:
一、等差数列的通项公式
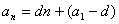 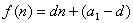
特征:
1° 等差数列的通项公式是关于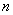 的一次函数,n是自变量, 的一次函数,n是自变量, 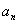 是函数 是函数
2° 如果通项公式是关于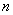 的一次函数,则该数列成等差数列; 的一次函数,则该数列成等差数列;
证明:若
它是以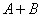 为首项, 为首项, 为公差的等差数列。 为公差的等差数列。
3° 图象是直线 上一些等间隔的点,公差d是该直线的斜率. 上一些等间隔的点,公差d是该直线的斜率.
4° 公式中若  则数列递增, 则数列递增,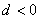 则数列递减; 则数列递减;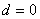 则数列为常数列 则数列为常数列
图像见教材P13页
等差数列与一次函数的异同:
|
|
等差数列 |
一次函数 |
|
解析式 |
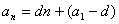 (n∈N+) (n∈N+)
|
f(x)=kx+b (k≠0) |
|
不同点 |
1、定义域为N+,
2、图像是直线 上一些等间隔的点. 上一些等间隔的点.
3、d=0,{an}为常数列. |
1、定义域为R,
2、图像是一条直线.
3、k≠0. | |

