|
第一章《集合》复习第一课时 集合的概念
一、教学目标:1、集合的含义与表示:了解集合的含义,体会元素与集合的“属于”关系。能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用。2、集合的基本关系:理解集合之间包含与相等的含义,能识别给定集合的子集(不要求证明集合的相等关系、包含关系)。了解全集与空集的含义。3、能运用上述概念解决一些问题。
二、重难点:重点:集合元素的特征、集合的三种表示方法、集合间的关系。
难点:正确把握集合元素的特征、进行集合的不同表示方法之间的相互转化。
三、教学方法:讲练结合,探析归纳。
四、教学过程
(一).知识点归纳
1.集合
①定义:某些指定的对象集在一起就成为一个集合,每个对象叫做集合的元素。
②表示
列举法:将集合中的元素一一列举出来,用大括号括起来,如{a,b,c}
描述法:将集合中的元素的共同属性表示出来,形式为:P={x∣P(x)}.
如: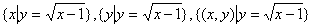
又如:{x︱x≥1}与{y ︱y=x2-2x+2}
图示法:用文氏图表示题中不同的集合。
③分类:有限集、无限集、空集。
④性质 确定性: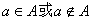 必居其一, 必居其一,
互异性:不写{1,1,2,3}而是{1,2,3},集合中元素互不相同,
无序性:{1,2,3}={3,2,1}
2.常用数集:实数集R 整数集Z 自然数集N 正整数集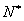 (或N+) 有理数集Q (或N+) 有理数集Q
3.元素与集合的关系: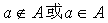
4.集合与集合的关系: ①子集:若对任意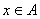 都 都 |

