【学习目标】 了解异面直线,公理4、及等角定理及它们的应用
【重点难点】公理4、及等角定理的理解及应用
【知识链接】公理1
公理2
公理3
1. 提出问题:同一平面上的两条直线位置关系有哪几种?
2. 按符号画出图形:a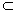 α,b∩α=A,A α,b∩α=A,A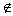 a a
3. 探究:教室内的哪些直线实例?有什么位置关系?
【学法指导】归纳推理
【学习过程】
一. 教学两条直线的位置关系:
实例探究 → 定义异面直线:不同在任何一个平面内的两条直线.
→ 以长方体为例,寻找一些异面直线? →性质:既不平行,又不相交。
→举例:教室内,日常生活中… →画法:以辅助平面衬托:(三种)
→讨论:分别在两个平面内的两条直线,是不是异面直线?
②讨论:空间两条直线的位置关系:(整理如下)

二、平行公理:
① 提出问题:平行于同一条直线的两条直线互相平行?
结论:
用数学符号表示为
例1:在空间四边形AB CD中,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:四边形EFGH是平行四边形。
练习:空间四边形ABCD,E、H分别是边AB、AD的中点,F、G分别是边CB、CD上的点,且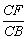 = =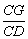 = =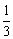 ,求证:EFGH是梯形。 ,求证:EFGH是梯形。
|

