|
2-4平面向量的坐标
一、教学目标:
1.知识与技能
(1)掌握平面向量正交分解及其坐标表示.
(2)会用坐标表示平面向量的加、减及数乘运算.
(3)理解用坐标表示的平面向量共线的条件.
2.过程与方法
教材利用正交分解引出向量的坐标,在此基础上得到平面向量线性运算的坐标表示及向量平行的坐标表示;最后通过讲解例题,巩固知识结论,培养学生应用能力.
3.情感态度价值观
通过本节内容的学习,使同学们对认识到在全体有序实数对与坐标平面内的所有向量之间可以建立一一对应关系(即点或向量都可以看作有序实数对的直观形象);让学生领悟到数形结合的思想;培养学生勇于创新的精神.
二.教学重、难点
重点: 平面向量线性运算的坐标表示及向量平行的坐标表示.
难点: 平面向量线性运算的坐标表示及向量平行的坐标表示.
三.学法与教学用具
学法:(1)自主性学习+探究式学习法:
(2)反馈练习法:以练习来检验知识的应用情况,找出未掌握的内容及其存在的差距.
教学用具:电脑、投影机.
四.教学设想
【创设情境】
(回忆)平面向量的基本定理(基底) 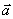 =λ1 =λ1 +λ2 +λ2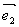
其实质:同一平面内任一向量都可以表示为两个不共线向量的线性组合.
【探究新知】
(一)、平面向量的坐标表示
1.在坐标系下,平面上任何一点都可用一对实数(坐标)来表示
思考:在坐标系下,向量是否可以用坐标来表示呢?
取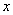 轴、 轴、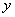 轴上两个单位向量 轴上两个单位向量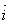 , , 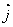 作基底,则平面内作一向量 作基底,则平面内作一向量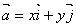  记作: 记作: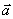 =(x, y) 称作向量 =(x, y) 称作向量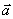 |

