|
赣马高级中学2011届高三考点突破专题十四
数形结合思想、坐标法应用(1)
032数形结合是,就是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的一种重要思想方法。
【自我提醒】
1.应用数形结合的思想,应注意以下数与形的转化
(1)集合的运算及韦恩图;(2)函数及其图象;(3)数列通项及求和公式的函数特征及函数图象;(4)方程(多指二元方程)及方程的曲线
2 实现数形结合常见的转化方式:
①实数与数轴上的点的对应关系;
②集合的运算及韦恩图;
③初等函数与图象的对应关系;
④方程与函数图像的对应关系。
⑤方程(多指二元方程)及方程的曲线
⑥以几何元素和几何条件为背景,建立起来的概念,如复数、三角函数等;
⑦所给的等式或代数式的结构含有明显的几何意义如斜率,两点间距离公式;
⑧数列通项、求和公式的函数特征及函数图象
⑨三角函数与函数图像之对应关系
【自我测试】
1.函数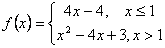 的图象和函数 的图象和函数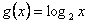 的图象的交点个数是 . 的图象的交点个数是 .
2.方程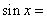 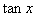 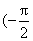 < < < <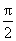 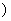 的解的个数 个; 的解的个数 个;
3.已知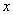 满足 满足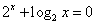 ,则 ,则 大小关系是 . 大小关系是 . 4.已知 |

