|
集合
【学法导航】
集合知识可以使我们更好地理解数学中广泛使用的集合语言,并用集合语言表达数学问题,运用集合观点去研究和解决数学问题。高考资源网
1.学习集合的基础能力是准确描述集合中的元素,熟练运用集合的各种符号,如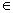 、 、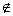 、 、 、 、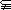 、=、 、=、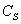 A、∪,∩等等; A、∪,∩等等;
2.强化对集合与集合关系题目的训练,理解集合中代表元素的真正意义,注意利用几何直观性研究问题,注意运用Venn图解题方法的训练,加强两种集合表示方法转换和化简训练;解决集合有关问题的关键是准确理解集合所描述的具体内容(即读懂问题中的集合)以及各个集合之间的关系,常常根据“Venn图”来加深对集合的理解,一个集合能化简(或求解),一般应考虑先化简(或求解);
3.确定集合的“包含关系”与求集合的“交、并、补”是学习集合的中心内容,解决问题时应根据问题所涉及的具体的数学内容来寻求方法。
① 区别∈与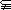 、 、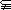 与 与 、a与{a}、φ与{φ}、{(1,2)}与{1,2}; 、a与{a}、φ与{φ}、{(1,2)}与{1,2};
② A B时,A有两种情况:A=φ与A≠φ。 B时,A有两种情况:A=φ与A≠φ。
③若集合A中有n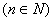 个元素,则集合A的所有不同的子集个数为 个元素,则集合A的所有不同的子集个数为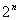 ,所有真子集的个数是 ,所有真子集的个数是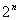 -1, 所有非空真子集的个数是 -1, 所有非空真子集的个数是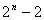 
④区分集合中元素的形式:
如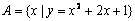 ; ;
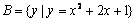 ; ;
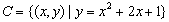 ; ;
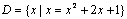 ; ;
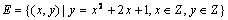 ; ;
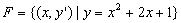 ; ;
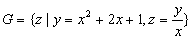 。 。
|

