|
20.垂径定理
知识考点:
1、垂径定理及其推论是指:一条直线①过圆心;②垂直于一条弦;③平分这条弦;④平分弦所对的劣弧;⑤平分弦所 对的优弧。这五个条件只须知道两个,即可得出另三个(平分弦时,直径除外),要求理解掌握。 对的优弧。这五个条件只须知道两个,即可得出另三个(平分弦时,直径除外),要求理解掌握。
2、掌握垂径定理在圆的有关计算和证明中的广泛应用。
精典例题:
【例1】如图,⊙O的直径AB和弦CD相交于E,若AE=2cm,BE=6cm,∠CEA=300,求:
(1)CD的长;
(2)C点到AB的距离与D点到AB的距离之比。
 分析:有关弦、半径、弦心距的问题常常利用它们构造的直角三角形来研究,所以连半径、作弦心距是圆中的一种常见辅助线添法。 分析:有关弦、半径、弦心距的问题常常利用它们构造的直角三角形来研究,所以连半径、作弦心距是圆中的一种常见辅助线添法。
解:(1)过点O作OF⊥CD于F,连结DO
∵AE=2cm,BE=6cm,∴AB=8cm
∴⊙O的半径为4 cm
∵∠CEA=300,∴OF=1 cm
∴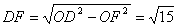 cm cm
由垂径定理得:CD=2DF=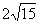 cm cm
(2)过C作CG⊥AB于G,过D作DH⊥AB于H,易求EF=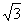 cm cm
∴DE= 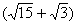 cm,CE= cm,CE=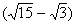 cm cm
∴
 【例2】如图,半径为 【例2】如图,半径为 2的圆内有两条互相垂直的弦AB和CD,它们的交点E到圆心O的距离等于1,则 2的圆内有两条互相垂直的弦AB和CD,它们的交点E到圆心O的距离等于1,则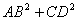 =( ) =( )
A、28 B、26 C、18 D、35 |

