第9计 数形开门 体美神丰
●计名释义
“有数无形少直观，有形无数入微难”.——这是华罗庚先生讲数形结合的意义.
“凭直观，图上看；想深入，解析出”.——这是专家们谈形与数各自的特征.
“遇式不用愁，请你先画图；看图莫着急，静心来分析”.——这是在讲数形互动.
“图形有形象，记数不易忘；解析有内功，看图静变动”.——这是在讲数形互补.
“观图见形美，初品数学味；想数内涵丰，数学色调浓”.这是美学家对数形的赞赏.
函数有图形——图象，轨迹有图象——图形，三角、几何就更不必说，集合有韦恩图，逻辑有方框图，组合、二项式有杨辉三角，如此等等.
然而，数形结合中的形，仅相对数而言.如几何中最简单的直线，平面等，现实生活中并不存在.
这里的形是数的象征，是精神的直观.现在有人把“函数图象”写成“函数图像”，这是对数形的大误，你怎么不把“想象”写成“想像”呢？
●典例示范
【例1】 若直线y=2a与函数y=|ax-1|（a>0，a≠1）的图象有两个公共点，则a的取值范围是 .
【解答】 函数y=|ax-1|= ，其图象由y=|ax|（a>0，a≠1）的图象下移一个单位得到.如图，当a>1时，直线y=2a与y=|ax-1|(a>0，a≠1)的图象仅一个交点； 当0时，当且仅当0<2a<1时，直线y=2a与y=|ax-1|（a>0，a≠1)的图象有两个公共点，解得a∈(0， ).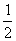
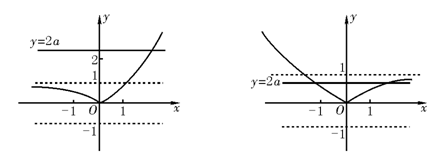
例1题解图
【评注】 本题也是有数无形，解法是“图形开门，体美神丰”.
|
