§14．2  轴对称变换

1.轴对称变换

知识要点

    1．由一个平面图形得到它的轴对称图形叫做轴对称变换．成轴对称的两个图形中的任何一个可以看着由另一个图形经过轴对称变换后得到．

    2．轴对称变换的性质：

    （1）经过轴对称变换得到的图形与原图形的形状、大小完全一样

    （2）经过轴对称变换得到的图形上的每一点都是原图形上的某一点关于对称轴的对称点．

    （3）连接任意一对对应点的线段被对称轴垂直平分．

    3．作一个图形关于某条直线的轴对称图形的步骤：

    （1）作出一些关键点或特殊点的对称点．

（2）按原图形的连接方式连接所得到的对称点，即得到原图形的轴对称图形．

典型例题

例：在锐角∠AOB内有一定点P，试在OA、OB上确定两点C、D，使△PCD的周长最短．

    分析：△PCD的周长等于PC+CD+PD，要使△PCD的周长最短，根据两点之间线段最短，只需使得PC+CD+PD的大小等于某两点之间的距离，于是考虑作点P关于直线OA和OB的对称点E、F，则△PCD的周长等于线段EF的长．

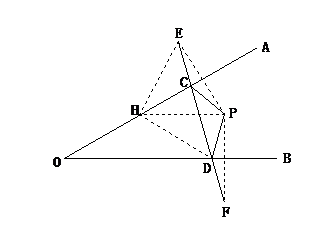作法：如图．①作点P关于直线OA的对称点E；

②作点P关于直线OB的对称点F；

③连接EF分别交OA、OB于点C、D．则C、D就是所要求作的点．

    证明：连接PC、PD，则PC=EC，PD=FD．

    在OA上任取异于点C的一点H，连接HE、HP、HD，则HE=HP．

∵△PHD的周长

=HP+HD+PD=HE+HD+DF>ED+DF=EF

而△PCD的周长

=PC+CD+PD=EC+CD+DF=EF

    ∴△PCD的周长最短．