|
 培英中学2008—2009学年度第二学期 培英中学2008—2009学年度第二学期
学生综合素质评定初二数学期中学业水平检测
一、单项选择题。(每题3分,共24分)
1.若分式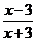 的值为0,则x的值为( ) 的值为0,则x的值为( )
A、-3 B、3或-3 C、3 D、0
2.已知关于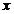 的函数 的函数 和 和 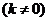 ,它们在同一坐 ,它们在同一坐
标系中的图象大致是( )
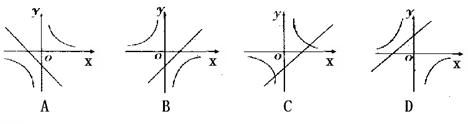
3.如果点(a,-2a)在双曲线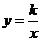 上,则此双曲线的图象在( ) 上,则此双曲线的图象在( )
(A)第一、二象限 (B)第一、三象限 (C)第二、四象限 (D)第三、四象限
4.在△ABC中,∠C=90°,若AC=3,BC=5,则AB=( )
A、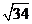 B、4 C、 B、4 C、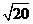 D、都不对 D、都不对
5.小明想做一个直角三角形的木架,以下四组木棒中,哪一组的三条能够刚好做成( )
A、9厘米,12厘米,15厘米; B、7厘米,12厘米,13厘米;
C、12 厘米,15厘米,17厘米; D、3 厘米,4厘米,7厘米。
6.已知一直角三角形的木版,三边的平方和为1800cm2,则斜边长为( )
A、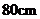 B、 B、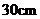 C、 C、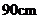 D、 D、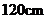
7.下列分式中与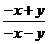 的值相等的分式是( ) 的值相等的分式是( )
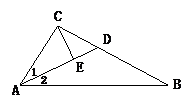 A. A.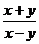 B. B.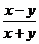 C.- C.-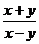 D.- D.-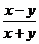
8.如图所示,已知∠1=∠2,AD=BD=4,
CE⊥AD,2CE=AC,那么CD的长是( )
A.2 B.3 C.1 D.1.5
二、填空题。(每题3分,共24分)
1.已知y与(2x+1)成反比例且当x=0时,y=2,那么当x=-1时,y=________
2.已知一次函数y=ax+b图象在一、二、三象限,则反比例函数y=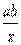 的函数值在每一个象限内随x的增大而__________。 的函数值在每一个象限内随x的增大而__________。
3.能成为直角三角形三边长的三个正整数叫勾股数(如3,4,5),请再写出一组不同的勾股数________________。
4.已知等腰三角形底边上的高为4,周长为16,则这个三角形面积为 。
5.测得一块三角形麦田三边长分别为9m,12m,15m,则这块麦田的面积为___________㎡。
 6.化简: 6.化简: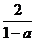 - -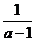 =________. =________.
7.如图,一棵大树在一次强台风中于离地面3m处
折断倒下,树干顶部在根部4米处,这棵大树在
折断前的高度为_________.
8.如果反比例函数的图象经过点(1,-2),那么这个反比例函数的 解析式为__________。
三、解答题:(共52分)
1.计算:(6分) (1)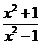 - -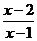 ÷ ÷ . .
2.解方程:(6分). (1)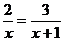
3.(8分)已知一个长方体的体积是100立方厘米,它的长是ycm,宽是
5cm,高是xcm.(1)写出用高表示长的函数式;(2)写出自变量
x的取值范围;(3)当x=3cm时,求y的值
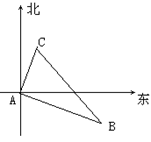
4.(8分)甲、乙两船同时从港口A出发,甲以12海里/时的速度向北
偏东35°航行,乙向南偏东55°航行。2小时后,甲到达C岛,
乙到达B岛,若C、B 相距40海里,问乙的速度是每小时多少海里?

5. (8分)如图,要从电线杆离地面8m处向地面拉一条长10m的
电缆,求地面电缆固定点A到电线杆底部B的距离.
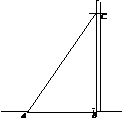
6.(8分)如图2,正比例函数y=x与反比例y=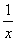 的图象相交于 的图象相交于
A、C两点,AB⊥x于B,CD⊥x轴于D,求四边形ABCD的面积。
7. (8分) 一游泳池长48m,小方和小朱进行游泳比赛,从同一
处出发,小方平均速度为3m/秒,小朱为3.1m/秒.但小朱一
心想快,不看方向沿斜线游,而小方直游,俩人到达终点的位
置相距14m.按各人的平均速度计算,谁先到达终点,为什么?
|

