|
函 数
1.专题综述
函数是高考数学的重要内容之一,函数的观点和思想方法贯穿整个高中数学的全过程,通过对2011年新课标卷的各省高考题的研究发现,本专题热点考点可总结为六类:一是分段函数的求值问题,二是函数的性质及其应用,三是基本函数的图像和性质,四是函数图像的应用,五是方程根的问题,六是函数的零点问题。涉及到得函数思想也是相当的丰富,如分段函数问题常与分类讨论思想相结合,有关方程根的情况判断常涉及函数与方程思想和等等价转化思想,研究函数的图像问题和基本函数的性质时常利用数形结合思想等。高考常命制两道小题,一道基础题目,出现在前5道题目中,常考查基本函数的性质或零点问题,另一道常以压轴的小题出现,常与方程的根或复合函数为背景考查,有一定的难度和灵活性。
2.考纲解读
(1)了解简单的分段函数并能简单应用;
(2)理解函数的单调性、最大(小)值及其几何意义,结合具体函数了解奇偶性的含义 ; ;
(3)理解指数(对数)函数的概念,理解指数(对数)函数的单调性,掌握指数(对数)函数图像经过的特殊点;结合常见的幂函数图像解决简单问题;掌握二次函数的三个表达形式,能够数形结合分析二次函数、一元二次方程、一元二次不等式三者之间的关系。
(4)会应用函数图像理解和研究函数的性质;
(5)根据具体函数的图像,能够运用二分法求相应方程的近似解;
(6)结合二次函数的图像,了解函数的零点与方程根的联系。
3 .2012年高考命题趋向
(1)以分段函数为表示形式考查求值问题是一类基础题目,常与指对数运算结合在一起,同时也考查学生能否 灵活运用分类讨论思想的解题能力。 灵活运用分类讨论思想的解题能力。
(2)以二次函数、分段函数、对数函数等为载体考查函数的性质是热点。研究函数的性质可充分利用函数的各种性质所反映的函数特点,来解决函数的相关问题.命题思路常以函数的各种性质相互交融,只有仔细审题,充分挖掘,把题目隐含的条件一一挖掘出来,综合利用性质才能达到解决问题的目的.
(3)与指数(对数)函数有关的综合问题的考查,以函数某个性质为核心,结合其他知识,把问题延伸,主要考查知识的综合运用和能力发展为目的.[来源:Z,xx,k.Com]
(4)函数图象的考查涉及的知识面广,形式灵活,经常以新面孔出现,在基本的初等函数图象熟练地掌握基础上,加以变换考查新函数的图象、性质等 . .
(5)利用转化思想解决方程问题,利用函数与方程思想解决函数应用问题,利用数形结合思想研究方程根的分布问题,是高考的热点和难点,常作为压轴的选择题的形式出现。
(6)函数的零点,二分法是新增内容,在高考中以选择题、填空题的形式考查的可能性较大。对于用二分法求方程的近似解应引起重视,由于步骤的可重复性,故可与程序框图相机合编写部分题目,这也是算法思想的的具体体现。解决由函数零点(方程根)的存在情况求参数的值或取值范围问题,关键是利用函数方程思想或数形结合思想,构建关于参数的方程或不等式求解.
4.高频考点解读
考点一 分段函数求值问题
【例1】[2011·福建卷] 已知函数f(x)=若f(a)+f(1)=0,则实数a的值等于( )
A.-3 B.-1 C.1 D.3
【答案】A
【解析】 由已知,得f(1)=2;又当x>0时,f(x)=2x>1,而f(a)+f(1)=0,∴f(a)=-2,且a<0,∴a+1=-2,解得a=-3,故选A.
【例2】[2011·陕西卷] 设f(x)=则f(f(-2))=________.
【答 案】-2 案】-2
【解析】 f(x)=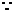 -2<0, -2<0,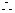 f(-2)=10-2; f(-2)=10-2;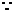 10-2>0, 10-2>0,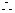 f(10-2)=lg10-2=-2. f(10-2)=lg10-2=-2.
【解题技巧点睛】求f(g(x))类型的函数值时,应遵循先内后外的原则,而对于分段函数的求值问题,必须依据条件准确地找出利用哪一段求解,特别地对具有周期性的函数求值要用好其周期性.
考点二 函数性质的基本应用
【例3】[2011·课标全国卷] 下列函数中,既是偶函数又在(0,+∞)单调递增的函数是( )
A.y=x3 B.y=|x|+1 C.y=-x2+1 D.y=2-|x|
【答案】B
【解析】 A选项中,函数y=x3是奇函数;B选项中,y=+1是偶函数,且在上是增函数;C选项中,y=-x2+1是偶函数,但在上是减函数;D选项中,y=2-|x|=|x|是偶函数,但在上是减函数.故选B.
【例4】[2011·辽宁卷] 若函数f(x)=为奇函数,则a=( )
A. B. C. D.1
【答案】A
【解析】 法一:由已知得f(x)=定义域关于原点对称,由于该函数定义域为,知a=,故选A.
法二:∵f(x)是奇函数,∴f(-x)=-f(x),又f(x)=,
则=,因函数的定义域内恒成立,可得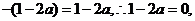 a=. a=.
【例5】【2011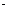 新课标全国】函数 新课标全国】函数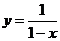 的图像与函数 的图像与函数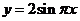 ( (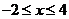 )的图像所有交点的横坐标之和等于( ). )的图像所有交点的横坐标之和等于( ).
A.2 B.4 C.6 D.8
 【解题技巧点睛】在解决与函数性质有关的问题中,如果结合函数的性质画出函数的简图,根据简图进一步研究函数的性质,就可以把抽象问题变得直观形象、复杂问题变得简单明了,对问题的解决有很大的帮助. (1)一般的解题步骤:利用函数的周期性把大数变小或小数变大,然后利用函数的奇偶性调整正负号,最后利用函数的单调性判断大小; (2)画函数草图的步骤:由已知条件确定特殊点的位置,然后利用单调性确定一段区间的图象,再利用奇偶性确定对称区间的图象,最后利用周期性确定整个定义域内的图象. 【解题技巧点睛】在解决与函数性质有关的问题中,如果结合函数的性质画出函数的简图,根据简图进一步研究函数的性质,就可以把抽象问题变得直观形象、复杂问题变得简单明了,对问题的解决有很大的帮助. (1)一般的解题步骤:利用函数的周期性把大数变小或小数变大,然后利用函数的奇偶性调整正负号,最后利用函数的单调性判断大小; (2)画函数草图的步骤:由已知条件确定特殊点的位置,然后利用单调性确定一段区间的图象,再利用奇偶性确定对称区间的图象,最后利用周期性确定整个定义域内的图象.
考点三 基本函数的性质与图像
【例6】[2011·天津卷] 已知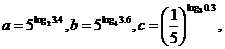 则( ). 则( ).
A.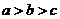 B. B.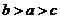 C. C.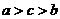 D. D.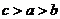
【答案】C
【解析】根据对数函数的运算性质可知: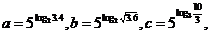 再由指数函数 再由指数函数
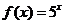 为单调递增函数,因为 为单调递增函数,因为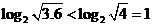 . .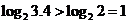 , ,
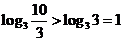 ,且 ,且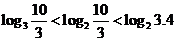 ,所以 ,所以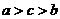 . .
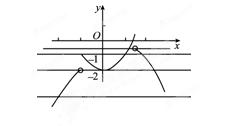 【例7】[2011·天津卷] 对实数a和b,定义运算“⊗”:a⊗ 【例7】[2011·天津卷] 对实数a和b,定义运算“⊗”:a⊗ b=设函数f b=设函数f (x)=(x2-2)⊗(x- (x)=(x2-2)⊗(x- x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( ) x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
A.(-∞,-2]∪ B.(-∞,-2]∪
C.∪ D.∪
【答案】B
【解析】本题考查二次函数的性质和图像。
f(x)==
则f的图象如图:
∵y=f(x)-c的图象与x轴恰有两个公共点,
∴y=f(x)与y, =c的图象恰有两个公共点,
由图象知c≤-2,或-1<c<-.
考点四 函数图像的应用
【例8】[2011·陕西卷] 设函数f(x)(x∈R)满足f(-x)=f(x),f(x+2)=f(x),则y=f(x)的图像可能是( )
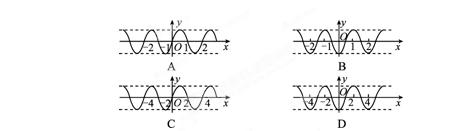
【答案】B
【解析】 由f(-x)=f(x)可知函数为偶函数,其图像关于y轴对称,可以结合选项排除A、C,再利用f(x+2)=f(x),可知函数为周期函数,且T=2,必满足f(4)=f(2),排除D,故只能选B.
【例9】 [2011·课标全国卷] 已知函数y=f(x)的周期为2,当x∈[-1,1]时f(x)=x2,那么函数y=f(x)的图像与函数y=|lgx|的图像的交点共有( )
A.10个 B.9个 C.8个 D.1个
【答案】A
【解析】考查数形结合思想,在同一直角坐标系中作出两个函数的图像,故下图.容易判断出两函数图像的交点个数为10个,故选择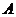 . .
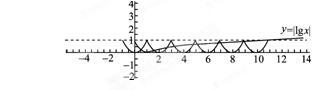
【解题技巧点睛】函数图象分析类试题,主要就是推证函数的性质,然后根据函数的性质、特殊点的函数值以及图象的实际作出判断,这类试题在 考查函数图象的同时重点是考查探究函数性质、用函数性质分析问题和解决问题的能力.利用导数研究函数的性质、对函数图象作出分析判断类的试题,已经逐渐成为高考的一个命题热点。 考查函数图象的同时重点是考查探究函数性质、用函数性质分析问题和解决问题的能力.利用导数研究函数的性质、对函数图象作出分析判断类的试题,已经逐渐成为高考的一个命题热点。
考点五 与方程根的相关问题
【例10】【2011 陕西】设 陕西】设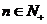 ,一元二次方程 ,一元二次方程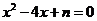 有整数根的充要条件是 有整数根的充要条件是
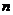 = . = .
【答案】 3或4.
【解析】直接利用求根公式进行计算,然后用完全平方数、整除等进行判断计算.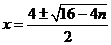 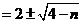 ,因为 ,因为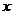 是整数,即 是整数,即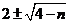 为整数,所以 为整数,所以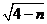 为整数,且 为整数,且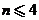 ,又因为 ,又因为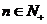 ,取 ,取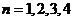 ,验证可知 ,验证可知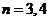 符合题意;反之 符合题意;反之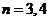 时,可推出一元二次方程 时,可推出一元二次方程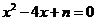 有整数根. 有整数根.
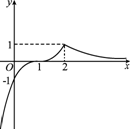
【例11】[2011·北京卷] 已知函数f(x)=若关于x的方程f(x)=k有两个不同的实根,则实数k的取值范围是________.
【答案】(0,1)
【解析】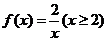 单调递减且值域为(0,1], 单调递减且值域为(0,1],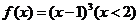 单调递增 单调递增
且值域为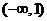 ,函数f(x)的图象如图所示,故 ,函数f(x)的图象如图所示,故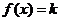 有两个不同的实根,则实数 有两个不同的实根,则实数
k的取值范围是(0,1).
考点六 函数零点问题
【例12】[2011·课标全国卷] 在下列区间中,函数f(x)=ex+4x-3的零点所在的区间为( )
A. B. C.  D. D.
 【答案】C 【答案】C
【解析】 因为f=e-2<0,f=e-1>0,所以f·f<0,
又因为函数y=ex是单调增函数,y=4x-3也是单调增函数,
所以函数f(x)=ex+4x-3是单调增函数,
所以函数f(x)=ex+4x-3的零点在内.[来源:学科网ZXXK]
【例13】[2011·山东卷] 已知函数f(x)=logax+x-b(a>0,且a≠1).当2<a<3<b<4时,函数f(x)的零点x0∈(n,n+1),n∈N*,则n=________.
【答案】 2 2
 【解析】 本题考查对数函数的单调性与函数零点定理的应用.因为2<a<3,所以loga2<1=logaaa3,因为3<b<4,所以b-2>1>loga2,b-3<1a3,所以f(2)·f(3)=(loga2+2-b)(loga3+3-b)<0,所以函数的零点在(2,3)上,所以n=2. 【解析】 本题考查对数函数的单调性与函数零点定理的应用.因为2<a<3,所以loga2<1=logaaa3,因为3<b<4,所以b-2>1>loga2,b-3<1a3,所以f(2)·f(3)=(loga2+2-b)(loga3+3-b)<0,所以函数的零点在(2,3)上,所以n=2.
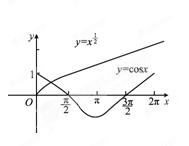
【例14】 [2011·陕西卷] 函数f(x)=-cosx在[0,+∞)内( )
A.没有零点 B.有且仅有一个零点C.有且仅有两个零点 D.有无穷多个零点
【答案】B
【解析】 在同一个坐标系中作出y=与y=cosx的图象如图,
由图象可得函数f(x)=-cosx在[0,+∞)上只有一个零点.
【解题技巧点睛】判断函数在某个区间上是否存在零点,要根据具体问题灵活处理,当能直接求出零点时,就直接求出进行判断;当不能直接求出时,可根据零点存在性定理进行判断;当用零点存在性定理也无法判断时可画出图象判断.
针对 训练 训练
一.选择题
1.【北京市朝阳区2011-2012学年度高三年级第一学期期中统一考试】
已知函数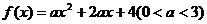 ,其图象上两点的横坐标 ,其图象上两点的横坐标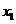 , ,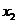 满足 满足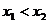 , ,
且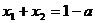 ,则有 ( ) ,则有 ( )
 A. A.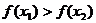 B. B. 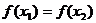
C.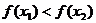 D. D.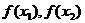 的大小不确定 的大小不确定
答案:C
解析: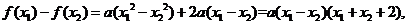
因为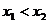 所以 所以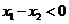 , ,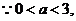 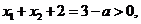
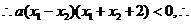 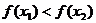
2.【2012年长春市高中毕业班第一次调研测试数学试题卷】
“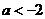 ”是“函数 ”是“函数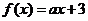 在区间 在区间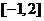 上存在零点”的 上存在零点”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件[来源:学科网]
答案:A
解析: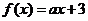 在区间 在区间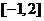 上存在零点,则 上存在零点,则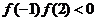 ,即 ,即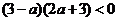 ,∴ ,∴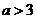 或 或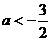 ,∴“ ,∴“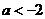 ”是“ ”是“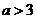 或 或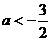 ”的充分不必要条件,∴“ ”的充分不必要条件,∴“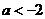 ”是“函数 ”是“函数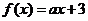 在区间 在区间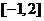 上存在零点”的充分不必要条件. 上存在零点”的充分不必要条件.
3.【银川一中2012届高三年级第四次月考】
若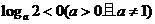 ,则函数 ,则函数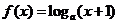 的图像大致是( ) 的图像大致是( )
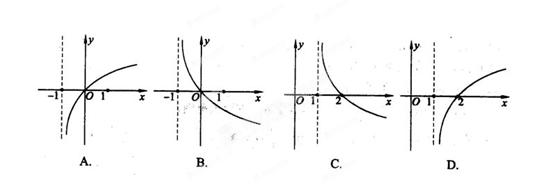 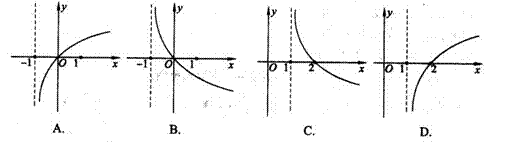
解析: 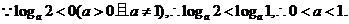 函数在定义域为减函数,将函数 函数在定义域为减函数,将函数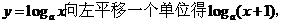 故答案为B。 故答案为B。
4.【银川一中2012届高三年级第四次月考】
设若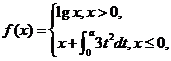 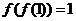 ,则 ,则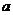 的值是( ) 的值是( )
A. -1 B. 2 C. 1 D.-2
解析: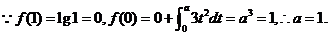
5.【安徽省示范高中2012届高三第二次联考】
实数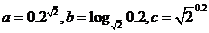 的大小关系正确的是( ) 的大小关系正确的是( )
A: 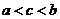 B: B: 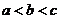 C: C: 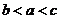 D: D: 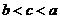
答案:C
解析:根据指数函数和 对数函数的性质, 对数函数的性质,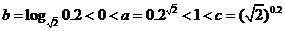 。 。
6.【安徽省示范高中2012届高三第二次联考】
函数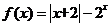 在定义域内零点的个数是( ) 在定义域内零点的个数是( )
(A)0 (B)1 (C)2 (D)3
答案:D
解析:在同一坐标系中画出函数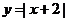 与 与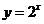 的图像,可以看到2个函数的图像在第二象限有2个交点,在第一象限有1个交点,所以函数 的图像,可以看到2个函数的图像在第二象限有2个交点,在第一象限有1个交点,所以函数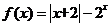 在定义域内有3个零点。 在定义域内有3个零点。
7.【河北省唐山市2012届高三上学期摸底考试数学】
若函数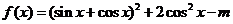 在 在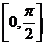 上有零点,则 上有零点,则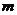 的取值范围为( ) 的取值范围为( )
A. 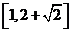 B. B. 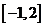 C. C. 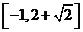 D. D. 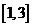
解析: 由函数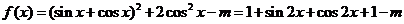
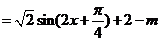 得在 得在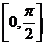 上的最大值是 上的最大值是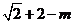 ,最小值是 ,最小值是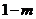
所以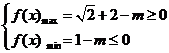 ,解得 ,解得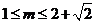 . .
8.【河北省唐山市2012届高三上学期摸底考试数学】[来源:Zxxk.Com]
已知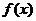 是奇函数,且 是奇函数,且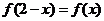 ,当 ,当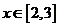 时, 时,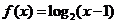 ,则当 ,则当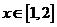 时 时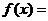 ( ) ( )
A. 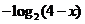 B. B. 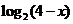 C. C. 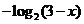 D. D. 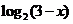
解析: 由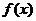 是奇函数,且 是奇函数,且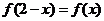 ,得 ,得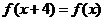 ,所以函数的周期 ,所以函数的周期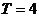
又因为当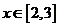 时, 时,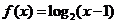 ,所以当 ,所以当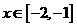 时, 时,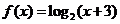 ,因为函数 ,因为函数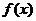 是奇函数,所以当 是奇函数,所以当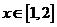 时 时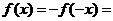 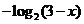 . .
9.【2012届江西省重点中学协作体高三第一次联考】
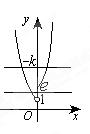 已知函数 已知函数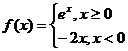 则关于 则关于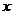 的方程 的方程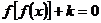 ,给出下列四个命题: ,给出下列四个命题:
①存在实数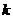 ,使得方程恰有1个不同实根;②存在实数 ,使得方程恰有1个不同实根;②存在实数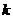 ,使得方程恰有2个不同实根;③存在实数 ,使得方程恰有2个不同实根;③存在实数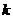 ,使得方程恰有3个不同实根;④存在实数 ,使得方程恰有3个不同实根;④存在实数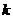 ,使得方程恰有4个不同实根;其中假命题的个数是 ( ) ,使得方程恰有4个不同实根;其中假命题的个数是 ( )
A.0 B.1 C.2 D.3
答案:C
解析: 当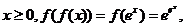 当 当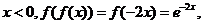
当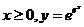 是增函数, 是增函数,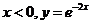 是减函数,由 是减函数,由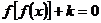 得 得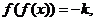
方程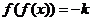 解的个数即 解的个数即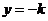 与 与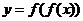 的图像交点的个数,由图像得当 的图像交点的个数,由图像得当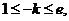 有1个解;当 有1个解;当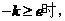 有2解。 有2解。
10.【2012年长春市高中毕业班第一次调研测试数学试题卷】
设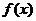 是定义在 是定义在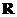 上的增函数,且对于任意的 上的增函数,且对于任意的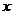 都有 都有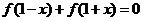 恒成立. 如果实数 恒成立. 如果实数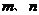 满足不等式组 满足不等式组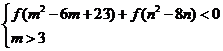 ,那么 ,那么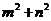 的取值范围是 的取值范围是
A.(3, 7) B.(9, 25) C.(13, 49) D. (9, 49) [来源:学。科。网Z。X。X。K]
答案:C
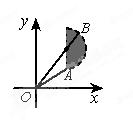 解析:由 解析:由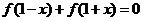 得 得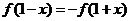 , ,
又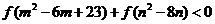 ,∴ ,∴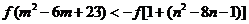 ,∴ ,∴ 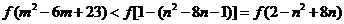 . .
∵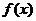 是 是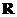 上的增函数,∴ 上的增函数,∴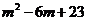 < <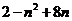 , ,
∴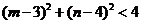
又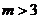 ,结合图象知 ,结合图象知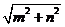 为半圆 为半圆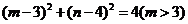 内的点到原点的距离,故 内的点到原点的距离,故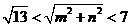 ,∴ ,∴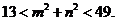
二.填空题
11.【2012年上海市普通高等学校春季招生考试数学试卷】
若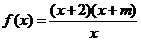 为奇函数,则实数 为奇函数,则实数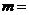 . .
解析: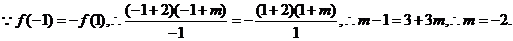
12.【北京市朝阳区2011-2012学年度高三年级第一学期期中统一考试】
已知函数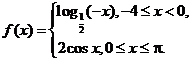 若方程 若方程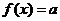 有解,则实数 有解,则实数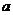 的取值范围是 __ _. 的取值范围是 __ _.
答案: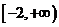
解析: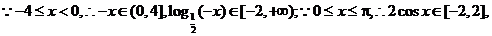 若方程 若方程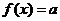 有解,即函数的值域即为 有解,即函数的值域即为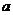 的范围,故实数 的范围,故实数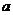 的取值范围是 的取值范围是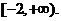
13.【2012年上海市普通高等学校春季招生考试数学试卷】
函数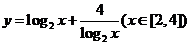 的最大值为 . 的最大值为 .
解析: 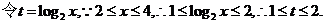 因对号函数 因对号函数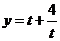 在区间[1,2]上单调递减,故当 在区间[1,2]上单调递减,故当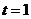 时函数取得最大值为5. 时函数取得最大值为5.
14.【2012年上海市普通高等学校春季招生考试数学试卷】
若不等式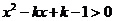 对 对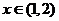 恒成立,则实数 恒成立,则实数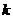 的取值范围是 . 的取值范围是 .
解析: 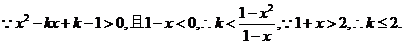
15.【北京市朝阳区2011-2012学年度高三年级第一学期期中统一考试】
设函数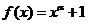 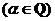 的定义域为 的定义域为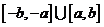 ,其中 ,其中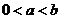 .若函数 .若函数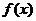 在区间 在区间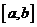 上的最大值为 上的最大值为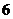 ,最小值为 ,最小值为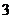 ,则 ,则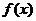 在区间 在区间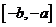 上的最大值与最小值的和为__ _. 上的最大值与最小值的和为__ _.
答案: 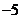 或 或
解析: 令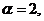 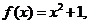 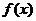 在区间 在区间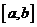 上的最大值为 上的最大值为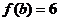 ,最小值为 ,最小值为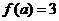 ,因 ,因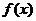 为偶函数,故 为偶函数,故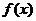 在区间 在区间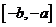 上的最大值与最小值为6和3,和为9;令 上的最大值与最小值为6和3,和为9;令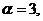 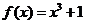 图象关于(0,1)点对称,设 图象关于(0,1)点对称,设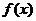 在区间 在区间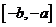 上的最大值 上的最大值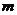 与最小值为 与最小值为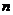 ,则有 ,则有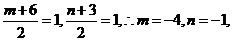 故 故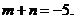
|

