|
7.3.1 多边形
主备人:张凤霞 审核人:史卫民 时间:
教学目标:
知识与技能
了解多边形及有关概念,理解正多边形及其有关概念。
过程与方法:
通过对多边形概念的探究,使学生体会从特殊到一般的认识问题的方法。
情感态度与价值观
通过对多边形的学习,感受数学与生活的联系。
教学重点:
多边形及有关概念。
教学难点:
区分凸凹多边形
导学过程:
一、复习引入
1、什么是三角形,什么是三角形的边、内角?
2、前面我们已经研究过三角形的有关概念,性质,那么边数大于三的多边形的概念和性质是什么呢?它们和三角形中的有关概念和性质是否有相似之处呢?让我们一起来探究一下
二、探究多边形的有关概念
1、学生观察教材79页的图7.3.1,它们是由哪些基本图形组成
的?
(学生观察图片,并进行讨论、交流后,抽学生发言)
2、你能说出生活中的多边形吗?
3、教师讲解多边形的有关概念。
(1)多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.按组成多边形的线段的条数分为三角形,四边形,五边形……如果一个多边形由n条线段组成,那么这个多边形叫做n边形.(一个多边形由几条线段组成,就叫做几边形.)
对概念的认识上,要让学生认识到“在平面内”这一点,三角形的概念中是没有这四个字的,这里多了几个字,想一想这是为什么?
(2)多边形的内角和外角:
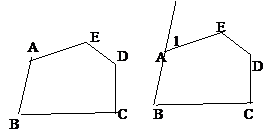 多边形相邻两边组成的角叫做多边形的内角,多边形的边与它的邻边的延长线组成的角叫做多边形的外角. 多边形相邻两边组成的角叫做多边形的内角,多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
如图:∠A、∠B、∠C、∠D、∠E是五边形ABCDE的内角,∠1是
ABCDE是五边形ABCDE的一个外角。
三、探究多边形的对角线的条数
1、学生阅读教材第80页第一自然段,理解多边形的对角线的定义。
2、教师提出问题:三角形有几条对角线,四边形呢?五边形,六边形,n边形呢?
先由学生自己动手操作,交流讨论,然后抽学生回答,师生共同归纳多边形对角线的条数: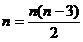
四、凸、凹多边形的概念及正多边形的概念
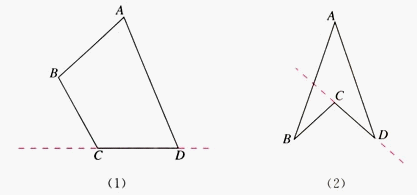
1、先让学生阅读教材第80页第二自然段的内容,然后教师讲解凸、凹多边形的概念。强调凸、凹多边形的概念区别,教师画几个多边形让学生进行凸、凹多边形的区分。
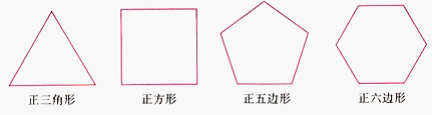
2、正多边形的概念
各个角都相等,各条边都相等的多边形叫做正多边形
五、练习:
1、教材第81页练习第1、2题。
2、判断题.
(1)由四条线段首尾顺次相接组成的图形叫四边形.( )
(2)由不在一直线上四条线段首尾次顺次相接组成的图形叫四边形.( )
(3)在同一平面内,四条线段首尾顺次连接组成的图形叫四边形.( )
六、课堂小结
引导学生总结本节课的相关概念。
七、布置作业:教材第84页习题7.3第1题。
达标测试:
1、已知一个多边形的对角线的条数是其边数的3倍,求这个多边形的边数。
2.今年寒假,实验中学安排全校师生假期进行社会实践活动,将每班分成3个组,每组派一名教师作为指导老师,为了加强同学间的协作,学校要求各班每两人之间(包括指导老师)每周至少通一次电话,现知八年级五班共有学生50名,那么该班师生之间每周至少要通几次电话?
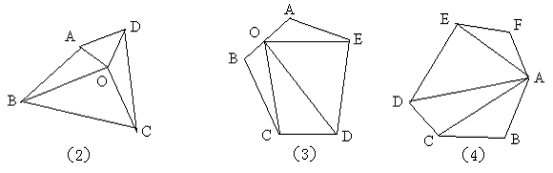
3、如图(2),O为四边形ABCD内一点,连接OA、OB、OC、OD可以得几个三角形?它与边数有何关系?
4、如图(3),O在五边形ABCDE的AB上,连接OC、OD、OE,可以得到几个三角形?它与边数有何关系?www.xkb1.com
5、如图(4),过A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
|

