一、学习目标

1、会根据实际问题中数量关系列方程解决问题，熟练掌握一元一次方程的解法．

2、培养学生数学建模能力，分析问题、解决问题的能力．

3、培养学生创新能力和挑战自我的意识，增强学生的学习兴趣。

二、重点：寻找实际问题中的等量关系，建立数学模型。；培养学生自己发现问题、解决问题的能力。难点：弄清题意，用列方程解决实际问题。。

三、学法指导：  自主学习，动手动脑

四、学习过程：

（一）复习引入

1解下列方程：

（1）

（2）

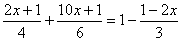
2.一项工作甲独做5天完成，乙独做10天完成，那么甲每天的工作效率是       ，乙每天的工作效率是        ，两人合作3天完成的工作量是          ，此时剩余的工作量是               。

3.一项工作甲独做a天完成，乙独做b天完成，那么甲每天的工作效率是       ，乙每天的工作效率是        ，两人合作3天完成的工作量是          ，此时剩余的工作量是                   。

（二）学生自主学习

问题1：某项工作，甲单独做需要4小时，乙单独做需要6小时，如果甲先做30分钟，然后甲、乙合作，问甲、乙合作还需要多久才能完成全部工作？

分析：

1 知识准备     关系：（1）工作量=       ×       

(2)工作时间=    ×     （3）工作效率=    ×    

 (3)注意：通常设完成全部工作的总工作量为  

2 设甲、乙合作还需要     小时才能完成全部工作

3 相等关系：                                   

列方程  :                                    

变式练习：一个道路工程，甲队单独施工9天完成，乙队单独做24天完成。现在甲乙两队共同施工3天，因甲另有任务，剩下的工程有乙队完成，问乙队还需几天才能完成？

（三）教师讲解

问题2 ：整理一批图书，由一个人做要40小时完成．现在计划由一部分人先做4小时，再增加两人和他们一起做8小时，完成这项工作．假设这些人的工作效率相同，具体应安排多少人工作？

分析：（1）人均效率（一个人做1小时完成的工作量）为           。

   （2）有x人先做4小时，完成的工作量为        。再增加2人和前一部分人一起做8小时，完成的工作量为           。