|
二.知识要点:
1.函数的单调性:
设函数在某区间内可导,则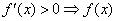 在该区间上单调递增; 在该区间上单调递增;
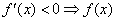 在该区间上单调递减. 在该区间上单调递减.
反之,若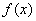 在某区间上单调递增,则在该区间上有 在某区间上单调递增,则在该区间上有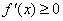 恒成立(但不恒等于0); 恒成立(但不恒等于0);
若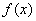 在某区间上单调递减,则在该区间上有 在某区间上单调递减,则在该区间上有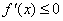 恒成立(但不恒等于0). 恒成立(但不恒等于0).
2.函数的极值:
(1)概念:函数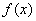 在点 在点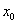 附近有定义,且若对 附近有定义,且若对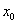 附近的所有点都有 附近的所有点都有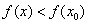 (或 (或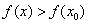 ),则称 ),则称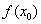 为函数的一个极大(小)值,称 为函数的一个极大(小)值,称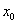 为极大(小)值点. 为极大(小)值点.
(2)求函数极值的一般步骤:
①求导数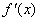 ;②求方程 ;②求方程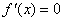 的根;③检验 的根;③检验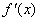 在方程 在方程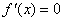 的根的左右的符号,如果是左正右负(左负右正),则 的根的左右的符号,如果是左正右负(左负右正),则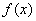 在这个根处取得极大(小)值. 在这个根处取得极大(小)值.
3.函数的最值:
①求函数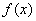 在区间 在区间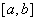 上的极值;②将极值与区间端点函数值 上的极值;②将极值与区间端点函数值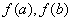 比较,其中最大的一个就是最大值,最小的一个就是最小值. 比较,其中最大的一个就是最大值,最小的一个就是最小值.
三.课前预习:
1.在下列结论中,正确的结论有 (  ) )
①单调增函数的导函数也是单调增函数; ②单调减函数的导函数也是单调减函数;
③单调函数的导函数也是单调函数; ④导函数是单调,则原函数也是单调的. |

