|
一.用导数求曲线的切线
函数 在 在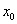 处导数的几何意义,就是曲线 处导数的几何意义,就是曲线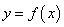 在点 在点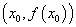 处切线的斜率,也就是说,曲线 处切线的斜率,也就是说,曲线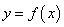 在点 在点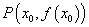 处切线的斜率是 处切线的斜率是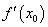 。于是相应的切线方程是: 。于是相应的切线方程是: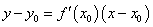 。 。
利用上述结论,可以求解曲线的切线以及相关的问题。
用求导法求曲线的切线的斜率是行之有效的方法,它不仅适用于二次曲线,对于任何可导函数都适用。如果要求的切线过某点,一定要注意验证这点是否在曲线上。如果这点在曲线上,可直接通过求这点的导数(斜率)来求切线方程,如果这点在曲线之外,一般需设切点,求出这点的导数,然后通过解方程组来确定切点,最后根据两点式确定切线方程。
二.用导数求瞬时速度
物体在时刻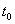 时的瞬时速度 时的瞬时速度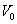 就是物体运动规律 就是物体运动规律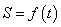 在 在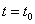 时的导数 时的导数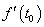 ,即有 ,即有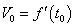 。 。
利用导数的这个物理意义,可以帮助我们获得按规律运动的物体的瞬时速度。
三.范例分析
例1.求过抛物线y=ax2+bx+c(a≠0)上一点P(x0,y0)处的切线方程,并由此证实抛物线的光学性质。
分析:为求斜率,先求导函数:y'=2ax+b,故切线方程为y-y0=(2ax0+b)(x-x0)
即 y=(2ax0+b)x-ax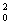 +c,亦即y=(2ax0+b)x-ax +c,亦即y=(2ax0+b)x-ax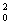 +c. +c.
抛物线焦点:F(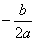 , ,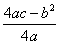 ),它关于切线的对称点之横坐标当x0,说明从焦点发出的光线射到(x0,y0)经抛物面反射后反射光线平行于对称轴,反之亦然。 ),它关于切线的对称点之横坐标当x0,说明从焦点发出的光线射到(x0,y0)经抛物面反射后反射光线平行于对称轴,反之亦然。
要求过曲线上一点处的切线方程,一般先求出该点的导数值(斜率),再用点斜式写出后化简,同时我们还可以据此写出该点处的法线方程。
解:显然,y0=ax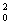 +bx0+c +bx0+c |

