|
21.2 二次根式的乘除
第2课时
【教学内容】
 = =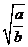 (a≥0,b>0),反过来 (a≥0,b>0),反过来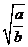 = = (a≥0,b>0)及利用它们进行计算和化简. (a≥0,b>0)及利用它们进行计算和化简.
【教学目标】
1、 知识与技能
掌握二次根式的除法法则,二次根式的除法运算和二次根式的化简。
理解最简二次根式的概念
2、过程与方法
利用具体数据,通过学生练习比较、猜想、论证二次根式的除法运算法则。
通过计算和化简掌握二次根式的除法运算法则、逆向思维运用逆向等式。
3、情感、态度与价值观
通过二次根式的计算和化简,培养学生对根式的运算兴趣,并掌握运算的技巧。
【教学重难点关键】
1.重点:
理解 = =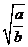 (a≥0,b>0), (a≥0,b>0),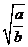 = = (a≥0,b>0)及利用它们进行计算和化简. (a≥0,b>0)及利用它们进行计算和化简.
2.难点:
二次根式的除法运算公式的双向使用
3、关键
发现规律,归纳出二次根式的除法法则.
【教学过程】
一、创设情境,导入新课
1、二次根式的乘法法则是什么?完成下列填空:
(1) 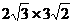 = = 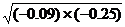 = =
(2) 若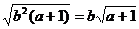 ,则a , b 。 ,则a , b 。
二次根式可以进行乘法运算,能否进行除法运算呢?
2、已知一个三角形的面积为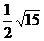 cm2,一条边长为 cm2,一条边长为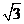 cm,求这条边上的高。 cm,求这条边上的高。
析:2×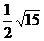 ÷ ÷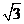
二、合作交流,探究新知
(一)二次根式的除法
[探究]1、计算下列各式,观察结果,你发现了什么规律?
(1) = = 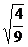 = =
(2)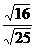 = = 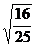 = =
(3)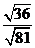 =________, =________,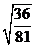 =________. =________.
2、用你发现的规律填空,并用计算器计算填空:
(1)  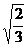 (2) (2) 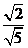 _____ _____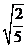
[猜想]二次根式的除法法则:
一般地,对于二次根式的除法规定: = =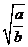 (a≥0,b>0), (a≥0,b>0),
你能用文字语言叙述这一法则吗?
二次根式相除,把被开方数相除,根指数不变。
[注意] 二次根式除法法则中b的取值范围!
[试一试](例4)计算:
(1) 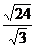 (2) (2) 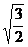 ÷ ÷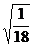
分析:利用 = =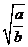 (a≥0,b>0)便可直接得出答案. (a≥0,b>0)便可直接得出答案.
解:(1) 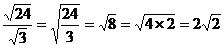
(2)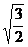 ÷ ÷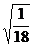 = =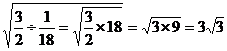
[做一做]计算:
(1)  (2) (2) 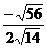 (3) (3) 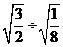 (4) (4) 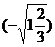 ÷ ÷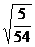
(5) 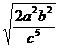 ÷ ÷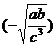 (a>0,b>0,c>0,) (a>0,b>0,c>0,)
答案:(1) 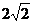 (2)-1 (3) 2 (2)-1 (3) 2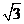 (4) (4) 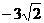 (5) (5) 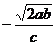
(二)商的算术平方根
[思考] 把 = =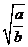 (a≥0,b>0),反过来就是, (a≥0,b>0),反过来就是,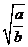 = = (a≥0,b>0) (a≥0,b>0)
利用它可以进行二次根式的化简。
[试一试](例5)化简
(1) 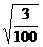 (2) (2) 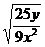
分析:直接利用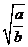 = = (a≥0,b>0)就可以达到化简之目的 (a≥0,b>0)就可以达到化简之目的
解:(1) 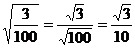 (2) (2) 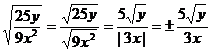
[注意] (2)中x的取值范围.
[做一做](例6)计算
(1) 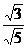 (2) (2) 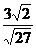 (3) (3) 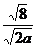
分析:利用 = =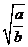 (a≥0,b>0)计算,发现被开开方数中的分母不是完全平方数或完全平方式。 (a≥0,b>0)计算,发现被开开方数中的分母不是完全平方数或完全平方式。
解:(1)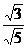 = =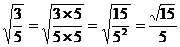 还有其他解法吗? 还有其他解法吗?
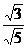 = =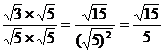
(2)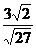 = =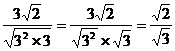 = =
(3)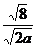 = =
观察以上各小题的最后结果,可以发现这些式子分母中不含二次根式。
(三)最简二次根式
[定义]如果二次根式有如下两个特点:(1) 被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式。那么我们把满足上述两个条件的二次根式,叫做最简二次根式。
[说明] 1、最简二次根式必须满足两个条件(1) 被开方数不含分母或小数;(2)被开方数中不含能开得尽方的因数或因式。
2、二次根式的计算或化简的结果,一般都要化成最简二次根式。
[想一想]判断下列二次根式,哪些是最简二次根式
(1) 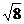 (2) (2) 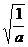 (3) (3) 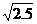 (4) (4) 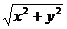 (5) (5)  (6) (6) 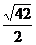 (7) (7) 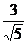
分析:利用定义即可判断(4)(5)(6)是最简二次根式。
[探究](教材第11页例7)如图,在Rt△ABC中,∠C=90°,AC=2.5cm,BC=6cm,求AB的长。
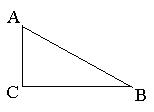
[分析]本题很容易想到运用勾股定理,关键就是计算。
[解]∵AB2=AC2+BC2 ∴AB=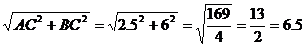 (cm) (cm)
∴AB的长为6.5cm.
[思考]现在可以解决本章引言的问题了。
式子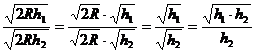
三、应用迁移、巩固提高
[练一练](教材第11页练习)
[试一试]已知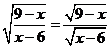 ,且x为偶数,求(1+x) ,且x为偶数,求(1+x)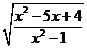 的值. 的值.
分析:式子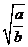 = = ,只有a≥0,b>0时才能成立. ,只有a≥0,b>0时才能成立.
因此得到9-x≥0且x-6>0,即6≤9,又因为x为偶数,所以x=8.
解:由题意得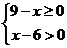 ,即 ,即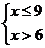 ∴6≤9 ∵x为偶数 ∴x=8 ∴6≤9 ∵x为偶数 ∴x=8
∴原式=(1+x)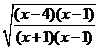 =(1+x) =(1+x)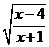 =(1+x) =(1+x)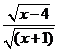 = =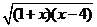
∴当x=8时,原式的值=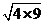 =6. =6.
四、总结反思、拓展升华
1、本节课学习的数学知识是:
二次根式的除法,掌握 = =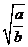 (a≥0,b>0)及其运用 (a≥0,b>0)及其运用
商的算术平方根,掌握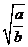 = = (a≥0,b>0)及其运用. (a≥0,b>0)及其运用.
最简二次根式
2、本节课学习的数学方法是将二次根式化为最简二次根式。二次根式化简口诀:
根内分母要跳墙,分解之后“指配双”,
跳出墙外要注意,仍要写在分母上。
五、布置作业
1.教材P12 习题21.2 中的2、7、8、9.
2.选用课时作业设计.
课时作业设计
一、选择题
1.计算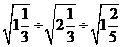 的结果是( ). 的结果是( ).
A.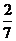 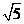 B. B.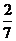 C. C.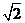 D. D.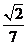
2.阅读下列运算过程: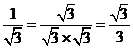 , , 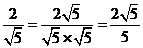
数学上将这种把分母的根号去掉的过程称作“分母有理化”,那么,化简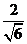 的结果是( ). 的结果是( ).
A.2 B.6 C.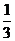 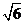 D. D.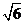
二、填空题
1.分母有理化:(1) 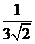 =_________;(2) =_________;(2) 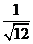 =________;(3) =________;(3) 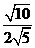 =______. =______.
2.已知x=3,y=4,z=5,那么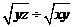 的最后结果是_______. 的最后结果是_______.
3.设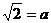 , ,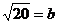 ,则用a、b的代数式表示 ,则用a、b的代数式表示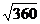 应为 应为
三、综合提高题
1.有一种房梁的截面积是一个矩形,且矩形的长与宽之比为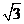 :1,现用直径为3 :1,现用直径为3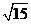 cm的一种圆木做原料加工这种房梁,那么加工后的房染的最大截面积是多少? cm的一种圆木做原料加工这种房梁,那么加工后的房染的最大截面积是多少?
2.计算
(1)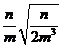 ·(- ·(-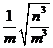 )÷ )÷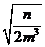 (m>0,n&, , gt;0) (m>0,n&, , gt;0)
(2)-3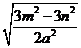 ÷( ÷( )× )×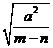 (a>0) (a>0)
(3) 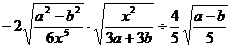
3.已知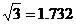 , ,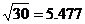 ,不用计算器求 ,不用计算器求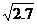 的值。 的值。
参考答案:
一、1.A 2.C
二、1.(1) 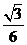 ;(2) ;(2) 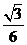 ;(3) ;(3) 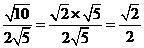
2.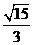
3.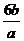
三、1.设:矩形房梁的宽为x(cm),则长为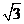 xcm,依题意, xcm,依题意,
得:(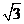 x)2+x2=(3 x)2+x2=(3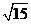 )2, )2,
4x2=9×15,x=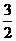 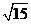 (cm), (cm),
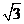 x·x= x·x=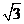 x2= x2=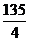 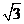 (cm2). (cm2).
2.(1)原式=-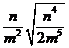 ÷ ÷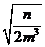 =- =-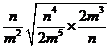
=-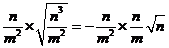 =- =-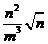
(2)原式=-2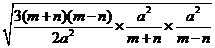 =-2 =-2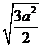 =- =-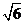 a a
(3)原式=(-2×1÷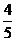 ) )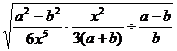
= 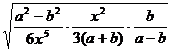 = = 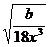 = =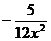 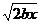
3.∵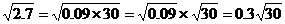
又∵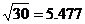 ∴ ∴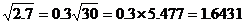 |

