|
青岛二中中考二轮复习--化归思想
Ⅰ、专题精讲:
数学思想是数学内容的进一步提炼和概括,是对数学内容的种本质认识,数学方法是实施有关数学思想的一种方式、途径、手段,数学思想方法是数学发现、发明的关键和动力.抓住数学思想方法,善于迅速调用数学思想方法,更是提高解题能力根本之所在.因此,在复习时要注意体会教材例题、习题以及中考试题中所体现的数学思想和方法,培养用数学思想方法解决问题的意识.
初中数学的主要数学思想是化归思想、分类讨论思想、数形结合思想等.本专题专门复习化归思想.所谓化归思想就是化未知为已知、化繁为简、化难为易.如将分式方程化为整式方程,将代数问题化为几何问题,将四边形问题转化为三角形问题等.实现这种转化的方法有:待定系数法、配方法、整体代人法以及化动为静、由抽象到具体等.
Ⅱ、典型例题剖析
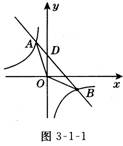 【例1】(嘉峪关,8 分)如图3-1-1,反比例函数y=-与一次函数y=-x+2的图象交于A、B两点. 【例1】(嘉峪关,8 分)如图3-1-1,反比例函数y=-与一次函数y=-x+2的图象交于A、B两点.
(1)求 A、B两点的坐标;
(2)求△AOB的面积.
解:⑴解方程组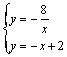 得 得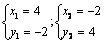
所以A、B两点的坐标分别为A(-2,4)B(4,-2
(2)因为直线y=-x+2与y轴交点D坐标是(0, 2), |

