|
)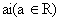 是纯虚数; 是纯虚数;
(2)在复平面内,原点也在虚轴上;
分析:先判断正误,若错误考虑如何纠错?或直接改正或举反例试之。
(1)错误。因为当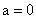 时,不是纯虚数。[来源:Zxxk.Com] 时,不是纯虚数。[来源:Zxxk.Com]
(2)错误。因为原点不在虚轴上。
探究性问题
已知关于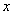 的方程 的方程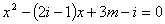 有实根,求实数 有实根,求实数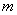 的取值。 的取值。
分析:注意不能用判别式△来解。
如:∵ 方程有实根
∴ 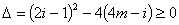
错误的原因是虚数不能比较大小,因此 涉及到大小问 涉及到大小问 题的概念和理论如与不等式有关的判别 题的概念和理论如与不等式有关的判别
 解:设方程的实根 解:设方程的实根 为x0,则 为x0,则
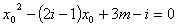
整理得: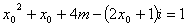
由复数相等的条件知:
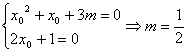
复数的分类例题
例 实数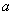 分别取什么值时,复数 分别取什么值时,复数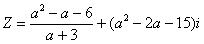 是(1 是(1 ) ) 实数(2)虚数(3)纯虚数。 实数(2)虚数(3)纯虚数。
解 :实部 :实部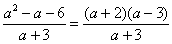 ,虚部 ,虚部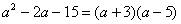
(1)当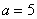 时,Z是实数;(2)当 时,Z是实数;(2)当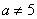 ,且 ,且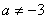 时,Z是虚数;(3)当 时,Z是虚数;(3)当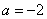 或 或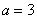 时是纯虚数. 时是纯虚数.
复数的相等 例题 例题
例 设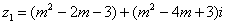 ( (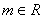 ), ),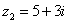 ,当 ,当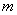 取何值时,(1) 取何值时,(1)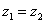 ;(2) ;(2)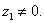
分析:复数相等的充要条件,提供了将复数问题转化为实数问题的依据,这是解复数问题常用的思想方法,这个题就可利用复数相等的充要条件来列出关于实数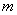 的方程,求出 的方程,求出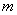 的值. 的值.
解:(1)由可得:
 解之得 解之得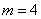 , ,
即:当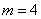 时 时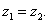
(2)当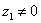 可得: 可得: |

