|
1.1 多项式的因式分解
教学目标
1.了解分解因式的意义,以及它与整式乘法的相互关系.
2.感受因式分解在解决相关问题中的作用.
3.通过因式分解培养学生逆向思维的能力。
重点与难点
重点:理解分解因式的意义,准确地辨析整式乘法与分解因式这两种变形。
难点:对分解因式与整式关系的理解
教学过程
一创设情境,导入新课
1 回顾整式乘法和乘法公式
填空:
计算:(1)2ab(3a+4b-1)=_________, (2)(a+2b)(2a-b)=__________
(3)(x-2y)(x+2y)=__________;(4) 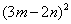 =_____________ =_____________
(5) 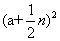 =________ =________
2 你会解方程: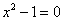 吗? 吗?
估计学生会想到两种做法:(1)一是用平方根的定义,(2)二是:解:(x+1)(x-1)=0,根据两个因式相乘等于0,必有一个因式等于0,得到:x+1=0或者x-1=0,因此:得x=1或-1
指出:把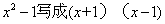 叫因式分解,为什么要把一个多项式因式分解呢?这节课我们来学习这个问题。 叫因式分解,为什么要把一个多项式因式分解呢?这节课我们来学习这个问题。
二 合作交流,探究新知
1 因式的概念
(1)说一说:
6=2×___, 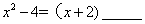 , ,
(2)指出:对于6与2,有整数3使得6=2×3,我们把2叫6的一个因数,同理,3也是6的一个因数。
类似的:对于整式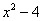 与x+2,有整式x-1使得 与x+2,有整式x-1使得 ,我们把x+2叫多项式 ,我们把x+2叫多项式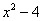 的一个因式,同理,x-2也叫多项式 的一个因式,同理,x-2也叫多项式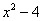 的一个因式。 的一个因式。 |

