|
第16课时平面与平面的位置关系习题课
分层训练
1.在四面体的各个面中, 直角三角形的个数最多的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
2.在正方体AC1中, M为DD1的中点, O为ABCD的中点, P为棱A1B1上的任一点, 则直线OP与AM所成的角为 ( )
A. 30° B. 45° C. 60°D. 90°
3.已知P是△EFG所成平面外一点, 且PE=PG, 则点P在平面EFG内的射影一定在△EFG的 ( )
A. ∠FEG的平分线上
B. 边EG的高上
C. 边EG的中线上
D. 边EG的垂直平分线上
4. PA⊥矩形ABCD所在的平面, AB=3 , BC=4 , PA=4 , 则P到CD的距离为________ . AD到平面PBC的距离____________ .
5. 已知P为锐二面角α- l –β棱上一点,PQ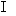 α,PQ与 α,PQ与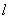 成45°角,与β成30°角, 则二面角α- l –β的大小 。 成45°角,与β成30°角, 则二面角α- l –β的大小 。
6.已知PA⊥矩形ABCD所在平面, M、N分别是AB、PC的中点.
(1)求证: MN⊥CD ;
(2)若∠PDA=45°, 求证: MN⊥平面PCD .
7.如图, 长方体AC1中, 已知AB=BC=a , BB1=b(b>a), 连结BC1 , 过B1作B1E⊥BC1, 交CC1于E , 交BC于Q , 求证: AC1⊥平面EB1D1 .
拓展延伸
已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=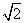 ,AF=1,M是线段EF的中点, ,AF=1,M是线段EF的中点,
(1).求证:AM//平面BDE
(2).求二面角A-DF-B的大小
(3).使在线段AC上确定一点P,使得PF与BC所成的角为60°
|

