|
平面向量 (B卷)
说明:试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入题后括号内,第Ⅱ卷可在各题后直接作答.共100分,考试时间90分钟.
第Ⅰ卷(选择题,共30分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列四个命题中,正确命题的个数是( )
①共线向量是在同一条直线上的向量 ②若两个向量不相等,则它们的终点不可能是同一点 ③与已知非零向量共线的单位向量是唯一的 ④四边形ABCD是平行四边形的充要条件是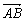 与 与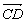 , ,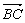 与 与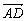 分别共线 分别共线
A.1 B.2 C.3 D.4
【解析】 平行向量即共线向量,不一定在同一条直线上,故①错;不等向量的终点可相同,故②错;与已知非零向量共线的单位向量有两个,一个同向,一个反向,故③错.
【答案】 A
2.在四边形ABCD中,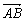 =a+2b, =a+2b,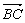 =-4a-b, =-4a-b,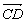 =-5a-3b,其中a、b不共线,则四边形ABCD为( ) =-5a-3b,其中a、b不共线,则四边形ABCD为( )
A.平行四边形 B.矩形 C.梯形 D.菱形
【解析】 ∵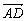 = =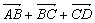 =-8a-2b=2 =-8a-2b=2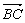 ,∴ ,∴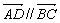 . .
∴四边形ABCD为梯形.
【答案】 C
3.任给a,b,则恒有( )
A.|a+b|=|a|+|b| B.|a-b|=|a|-|b|
C.|a-b|≤|a|+|b| D.|a-b|≤|a|-|b|
【答案】 C
4.下面三种说法中,正确的说法是( )
①一个平面内只有一对不共线的向量可作为表示该平面的所有向量的基底 ②一个平面内有无数多对不共线向量可作为表示该平面内的所有向量的基底 ③零向量不可作为基底中的向量
A.①② B.②③ C.①③ D.①②③
【解析】 任何一对不共线向量都可作为平面内所有向量的基底,基底有无穷多对,0与任何向量共线,所以不能作为基底中的向量,∴①错,②③对.
【答案】 B
5.已知命题p:非零向量a、b、c满足a+b+c=0;命题q:表示a、b、c的有向线段可构成三角形,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
【答案】 D
6.在△ABC中,AD、BE、CF分别是BC、CA、AB边上的中线,G是它的交点,则下列等式中不正确的是( )
A.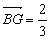 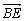 B. B.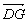 = =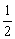 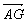
C.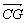 =-2 =-2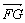 D. D.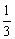 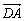 + +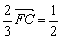 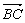
【解析】 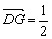 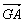 ≠ ≠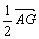 ,∴B不正确;A、C正确易得;对于D, ,∴B不正确;A、C正确易得;对于D,
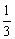 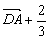 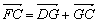 = =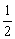 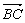 ,故D正确. ,故D正确.
|

