|
正余弦定理的应用-同步分层能力测试题
A组
一.填空题(本大题共8小题,每小题5分,共40分)
1.某人朝正东方向走了x km后,向左转1500后,再向前走了3 km,结果他离出发点恰好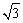 km,那么x= 。 km,那么x= 。
1.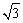 或2 或2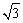 . 提示:由余弦定理知3=x2+32-6xcos300,解得x= . 提示:由余弦定理知3=x2+32-6xcos300,解得x=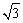 或2 或2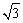 . .
2.在△ABC中,已知2sinAcosB=sinC,那么△ABC的形状是 三角形。
2.等腰。提示:由2sinAcosB=sinC,知2sinAcosB=sin(A+B),
∴2sinAcosB=sinAcosB+cosAsinB.即cosAsinB-sinAcosB=0. ∴sin(B-A)=0, ∴B=A.
3.一飞机沿水平方向飞行,在位置A处测得正前下方地面目标C的俯角为30°,向前飞行了10000米,到达位置B时测得正前下方地面目标C的俯角为75°,这时飞机与地面目标的距离为 米.
3.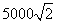 。提示:由正弦定理得 。提示:由正弦定理得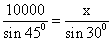 ,得x= ,得x=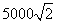 . .
4.在平行四边形ABCD中,已知AB=1,AD=2,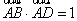 ,则 ,则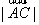 = . = .
4.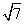 。提示: 。提示: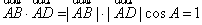 ,得cosA= ,得cosA=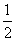 ,A=600.故B=1200。由余弦定理知:AC2=12+22-4cos1200=7, ,A=600.故B=1200。由余弦定理知:AC2=12+22-4cos1200=7, 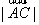 = =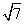 . .
5.在一次抗洪抢险中,某救生艇发动机突然发生故障停止转动,失去动力的救生艇在洪水
中漂行,此时,风向是北偏东300,风速是20 km/h;水的流向是正东,流速是20km/h,若
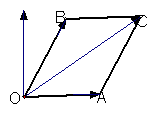 不考虑其他因素,救生艇在洪水中漂行的速度的方向为北偏东___________,大小为___________km/h. 不考虑其他因素,救生艇在洪水中漂行的速度的方向为北偏东___________,大小为___________km/h.
5.60 , 20 , 20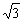 。提示:解法一:如图1,∠AOB=600, 。提示:解法一:如图1,∠AOB=600,
由余弦定理知OC2=202+202-800cos1200=1200,故OC=20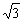 。 。
解法二:实质求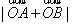 ,平方即可。 图1 ,平方即可。 图1
6.把一30厘米的木条锯成两段,分别做钝角三角行ABC的两边AB和BC,且∠ABC=120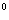 , ,
AB= 时,才能使第三条边AC最短。
6. 15.提示:在△ABD中,设AB=x(0<x<30) 由余弦定理,得
AC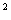 =x =x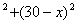 -2x(30-x)cos120 -2x(30-x)cos120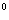 =900-30x+x =900-30x+x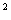 =(x—15) =(x—15)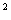 +675, +675,
所以 把AB锯成15厘米时第三条边AC最短
7. 在△ABC中,边a,b,c的对角分别为A、B、C,且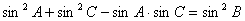 。则角B= 。 。则角B= 。
7.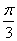 .提示:由正弦定理可设 .提示:由正弦定理可设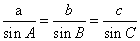 =k. =k.
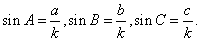 代入已知式,可得 代入已知式,可得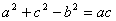 , ,
由余弦定理,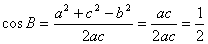 , , 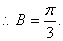 8. 如图2,在四边形ABCD中,已知AD^CD, AD=10, |

